Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Ряд геометрической прогрессии. Необходимый признак сходимости ряда. Гармонический ряд.

Ряд геометрической прогрессии - так называется ряд (бесконечная сумма), члены которого образуют геометрическую прогрессию с первым членом а0 и знаменателем прогрессии, равным q.

Необходимое условие сходимости ряда: Для сходимости ряда необходимо, чтобы последовательность (а_к) была бесконечно малой. Если ряд сходится, то его общий член стремится к нулю

Гармонический ряд — сумма, составленная из бесконечного количества членов, обратных последовательным числам натурального ряда:

.

Конечно, деньги не приносят счастья, но действуют чрезвычайно успокаивающе.

16. Признаки сравнения знакоположит. рядов.

Признак сравнения — утверждение об одновременности расходимости или сходимости двух рядов, основанный на сравнении членов этих рядов. Числовой ряд называется знакоположительным, если х_к>=0 для любого k

Первый признак сравнения. Пусть имеются два положительных ряда и , причём члены первого, начиная с некоторого места, не превосходят соответствующих членов второго: , Тогда из сходимости ряда B следует сходимость ряда A, а из расходимости ряда A следует расходимость ряда B. Второй признак сравнения. Пусть имеются два строго положительных ряда и (). Пусть существует конечный, отличный от нуля, предел 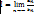(). Тогда ряды A и B сходятся или расходятся одновременно. Третий признак сравнения. Пусть имеются два строго положительных ряда и (). Пусть, начиная с некоторого места, т.е. для оказывается .

Тогда из сходимости ряда B следует сходимость ряда A, а из расходимости ряда A следует расходимость ряда B.