Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Линейные ДУ первого порядка.

Определение линейного уравнения первого порядка

Дифференциальное уравнение вида

где a(x) и f(x) − непрерывные функции x f(x)<>0, т.к. если оно будет равно нулю, это будет линейное однородное уравнение, которое является уравнением с разделяющимися переменными. Т. е. уравнение такого вида называтся линейным неоднородным дифференциальным уравнением первого порядка. Существует три способа решения этого уравнения:

• метод интегрирующего множителя;

• метод введения двух функций (Бернулли);

• метод вариации постоянной (Лагранжа).

33. Линейные однородные ДУ второго порядка.

Однородное уравнение второго порядка имеет вид:

Общим решением уравнения второго порядка называется такая функция которая при любых значениях с1 и с2 и является решением этого уравнения.

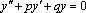Если коэффициенты p(x) и q(x) постоянны, т.е. не зависят от, то это уравнение называют уравнением с постоянными коэффициентами и записывают его так:

Определение. Уравнение которое получается из линейного однородного уравнения заменой функции y единицей, а y’ и y’’ - соответствующими степенями, называется характеристическим уравнением.

Известно, что квадратное уравнение имеет решение, зависящее от дискриминанта:, т.е. если D.o, то корни k1 и k2- действительные различные числа. Если D=0, то k1=k2. Если же D,0, т.е., то корни будут комплексными числами.