Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Система двух случайных величин

В практических задачах приходится сталкиваться со случаями, когда результат описывается двумя и более случайными величинами, образующими систему случайных величин (случайный вектор,) (х₁, х₂,..., х_n). Например, точка попадания снаряда имеет две координаты: х и у, которые можно принять за систему случайных величин, (х, у) оп­ределенных на одном и том же пространстве элементарных событий .

Закон распределения дискретной двумерной случайной величины можно представить в виде таблицы, характеризующей собой совокуп­ность всех значений случайных величин и соответствующих вероят­ностей:

	xl	x2		хn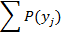
y1	Р(х1,у2)	Р(x2,y1)		P(xn,yi)	Р(у1)
y2	Р(х1у2)	Р(x2,y2)		Р(хn,у2)	P(y2)
ym	P(x1,ym)	Р(x2,ym)		Р(хn,уm)	P(ym)
	P(x1)	P(x2)		P(xn)

В общем случае двумерная случайная величина задается в виде интегральной функции: F(x, у) = Р(Х<х, Y<y), которая означает веро­ятность попадания двумерной случайной величины в квадрант левее и ниже точки с координатами (х, у).

Свойства интегральной функции:

Свойства интегральной функции:

1.F - не убывает и непрерывна слева по каждому аргументу;

2.F(- 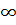, у)= F(x,- 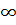)= F(- 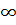, - 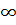)= 0;

F(+ 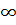, у)= F₂(y) - функция распределения случайной величины У;
F(x,+ 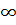)= F₁(x) — функция распределения случайной величины X.

4.F(+ 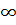,+ 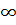)= 1.

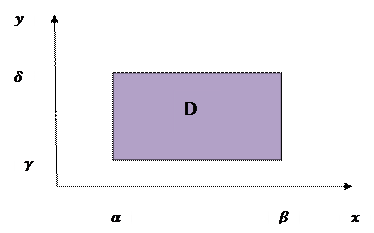
Вероятность попадания двумерной случайной величины в прямо­угольник определяется, исходя из определения интегральной функции двумерной случайной величины:

P(x,y)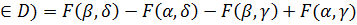

Случайные величины X, Y независимы, если F(x, у) = F₁(x) F₂(y). Дифференциальная функция системы двух непрерывных случайных ве­личин определяется как вторая смешанная производная функции рас­пределения:

=

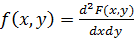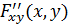
Свойства дифференциальной функции

1. f(x,y)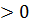

2.

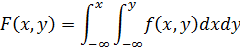
Геометрически свойство 2 означает, что объем тела, ограниченного поверхностью 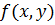и плоскостью XOY, равен 1. Если случайные величины х и у независимы, то

f(x,y)=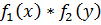

где – 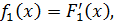безусловные законы распределения.

В противном случае:

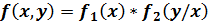или