Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Интервальные и точечные оценки параметров распределения

Пусть статистическая оценка служит оценкой параметра . Очевидно, что чем меньше по абсолютной величине разность , тем оценка точней. Поскольку случайная величина, то и эта разность также является случайной величиной. Потребуем, чтобы с вероятность v разность не превышала величину > 0.

Назовем точностью оценки, а – доверительной вероятностью. Перепишем последнее выражение в следующем виде:

Интервал называемый доверительным интервалом, с вероятностью включает в себя (покрывает) истинное значение параметра .

Поскольку случайная величина, то и границы доверительного интервала тоже являются случайными.

Основные понятия и алгоритм статистической проверки гипотез на основе статистических критериев

Статистическая гипотеза – подвергнутое статистической проверке предположение, относящееся к виду распределения случайных величин, наличию зависимостей между ними, принадлежности выборочных данных к одной генеральной совокупности.

Основную выдвинутую гипотезу H₀ принято называть нулевой, а гипотезу H₁, которая противоречит ей – конкурентной или альтернативной.

Для принятия или отклонения гипотез использует специальные показатели, которые называются статистическими критериями (некоторая функция от выборки).

Разобьем все множество значений критерия на две области. Одну из них, называемую критической, определим так, чтобы вероятность попадания в нее критерия, если нулевая гипотеза верна, была достаточно малой заранее заданной величиной:

Вся остальная часть числовой оси левее критической точки образует доверительную область.

Критическая область – совокупность значений критерия, при которых нулевую гипотезу отвергают.

Доверительная область (область принятия гипотезы) – совокупность значений критерия, при которых нулевую гипотезу принимают.

Могут возникнуть такие ошибки:

Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза.

Ошибка второго рода состоит в том, что будет принята неправильная гипотеза.

Вероятность ошибки первого рода 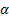называют уровнем значимости критерия.

Алгоритм статистической проверки гипотез путем использования критериев состоит в следующем: устанавливают уровень значимости 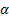и определяют критическую область, исходя из следующих соотношений:

1. Для правосторонней критической области.

при

2. Для левосторонней критической области.

при

3. Для двусторонней симметричной области.

при

при