Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Проверка гипотез с использованием непараметрических критериев

Подход не требует знания законов и параметров распределения, используют непараметрические критерии, которые выявляют путем выявления упорядоченности численных значений, полученных в результате наблюдений и установления между ними соответствий вид > или <.

Использование непараметрических критериев рассмотрим на примере критерия Вилкоксона применительно к задаче проверки гипотезы о принадлежности двух выборок к одной генеральной совокупности.

Пусть имеются две выборки элементы каждой из которых расположены по возрастанию.

1. Объединяют все элементы двух выборок в упорядоченную последовательность объемом .

2. Определим число инверсий U в выражении.

Инверсия – каждая пара значений для которых, иначе говоря число инверсий равно сумме чисел всех стоящий впереди каждого .

3. Будем считать, что число инверсий подчиняется нормальному закону со средним и дисперсией .

4. Если гипотеза верна, то U полученное экспериментально (по выборке) не должно сильно отличаться от .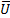

Если , то гипотезу отвергают.

5. Критическое значение числа инверсий при малых значениях m и n (< 14) для заданного уровня значимости 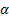табулированно.

Для больших значений m и n:

– квантиль (0,1)-нормального распределения порядка .

В практике экспериментальных ислледований часто возникает задача проверки гипотезы о том, что расположение элементов двух видов (0 и 1) носит случайный характер, т.е. является стохастически независимым. Просто решить эту задачу с помощью метода серий.

20 образцов горных пород, пренадлежащих к одной генеральной совокупности, были разделены на две равные группы. Одну подвергли механическому воздействию, а другую нет.

1 — 5,22 5,3 5,4 5,32 5,1 5,2 5,34 5,6 5,5 5,27

2 — 5,7 5,41 5,28 5,38 5,15 5,8 5,42 5,65 5,31 5,14

5,1(0) 5,14(1) 5,15(1) 5,2(0) 5,22(0) 5,27(0) 5,28(1) 5,29(0) 5,3(0) 5,31(1) 5,32(0) 5,38(1) 5,4(0) 5,41(1) 5,42(1) 5,5(0) 5,6(0) 5,65(1) 5,7(1) 5,8(1)

Элементы 0 и 1 в скобках рядом с числовыми значениями последовательности означают принадлежность соответственно к 1 и 2 группам. Выпишем их:

01100010010101100111 (*)

Серия – подряд идущие элементы одного типа. Здесь серий 12.

То есть 0 – первая серия, 11 – вторая и так далее.

Можно показать, что, если число элементов в последовательности (*) достаточно велико (n>10), то распределение числа серий близко к нормальному с характеристиками:

С вероятность 99,7% теоретическое число серий должно укладываться в интервал:

Для нашего примера при n=20 условие имеет вид:

Так как укладывается в границы , то можно сделать вывод о случайности расположения элементов в последовательности (*). Иначе говоря, последовательность измеренных значений признака носит случайный характер, и, следовательно, произведенное механическое воздействие не привело к значимым изменениям измеряемого признака.

Метод серий может быть использован также для проверки случайности последовательности изменения выборочных значений измеряемого признака. При этом определяют среднюю. Элементы, значения которых меньше средней, обозначают нулем, а элементы больше средней – единицей.