Читайте также:
|
При неограниченном увеличении числа опытов, ставящихся для наблюдения результатов поведения искомой величины,
испытаний в каждом опыте которой могут быть только 2 результата, которые образуют полную группу.
Пусть ставится n опытов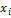 
, где i=1,2
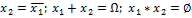
| Опыт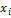
| Число наступлений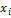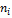 
| Вероятность появления 
|
| m | p |
| n-m | q=1-p |
Таким образом, необходимо установить наличие 2 результатов испытаний в целом. Определить условия проведения одного опыта. Выбрать 1 из результатов
при условии, что . Определить: событие А – искомое событие, n – число опытов, m – число опытов заканчивающихся событием , p=P() – вероятность в каждом опыте.
| n, m | A | Вероятность одного сложного |
| p=P(), q=1-p
|
события, состоящего в том, что в n испытаниях событие А наступит m раз и не наступит n-m раз по теореме умножению вероятностей независимых событий равна 
. Таких сложных событий может быть столько, сколько можно составить сочетаний из n элементов по m элементов т.е. 
. Так как эти сложные события несовместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равна сумме вероятностей всех возможных сложных событий, а так как вероятности всех этих событий одинаковы, то искомая вероятность равна вероятности одного сложного события, умноженная на их число: 
.
Формулу можно использовать, когда 
|
| m | p |
|
| n-m | q=1-p |
Таким образом, необходимо установить наличие 2 результатов испытаний в целом. Определить условия проведения одного опыта. Выбрать 1 из результатов
при условии, что . Определить: событие А – искомое событие, n – число опытов, m – число опытов заканчивающихся событием , p=P() – вероятность в каждом опыте.
Индикатор случайного события А U(A) – это дискретная случайная величина, которая равна 1 при осуществлении события А и 0 при осуществлении события не-А. 
|
| 
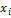
Числовые характеристики.
| ||
|
| 
| 
| |
| A | 
|
Свойства.
1. Любой результат испытаний в схеме Бернулли может быть представлен случайной величиной, которая представляется суммой индикаторов случайного события. 
2. По условию Лапласа 
Таким образом U(A) в схеме Бернулли является базовым элементом т.к. с его помощью можно построить математическую модель природного случайного события в схеме Бернулли.
средний результат этих опытов перестаёт быть случайным и может быть предсказан с большой степенью определённости. Формально – это совокупность законов и теорем, в каждой из которых устанавливается факт приближения большого числа опытов к некоторым постоянным, не случайным величинам.
Неравенство Чебышева. Любая случайная величина с множеством значений х: 
, имеющая закон распределения f(x) и конечные ограниченные числовые характеристики 
. Тогда: Вероятность того, что модуль отклонения значений случайной величины х от её математического ожидания превышает или равно числу 
будет меньше или равно отношения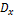 
к квадрату числа . 
Док-во: Пусть 
, изобразим на прямой случайных величин:
Из теории случайных величин 
Оценим интеграл «в средне»: 
Это отношение ограничивает сверху вероятности больших отклонений значений случайной величины от её математического ожидания.
Билет №13
Дата добавления: 2015-02-16; просмотров: 78 | Поможем написать вашу работу | Нарушение авторских прав |