Читайте также:
|
При испытаниях в схеме Бернулли относительная частота появления события А в каждом опыте сходится по вероятности, вероятностей появления этого события в каждом опыте.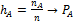 
Док-во: Смоделируем схему Бернулли индикатором случайного события А: 
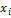
| Введём  , где
| ||
| 
| 
| |
| A | 
|
. Тогда 
. Зафиксируем n, найдём математическое
8. Совместные события – 2 события, которые могут происходить одновременно.
9. Независимые события – такие события, что появление одного из них не влияет на появление другого.
10. Зависимые события – такие события, что появление одного из них влияет на появление другого.
11. Равновозможные события - такие события, что появление одного из них не более возможно, чем появление другого.
12. Благоприятное событие – такое событие, которое влечёт за собой другое т. е. событие В произойдёт, ели произойдет А.
2. Закон больших чисел. Неравенство Чебышева. При неограниченном увеличении числа опытов, ставящихся для наблюдения результатов поведения искомой величины, средний результат этих опытов перестаёт быть случайным и может быть предсказан с большой степенью определённости. Формально – это совокупность законов и теорем, в каждой из которых устанавливается факт приближения большого числа опытов к некоторым постоянным, не случайным величинам.
Неравенство Чебышева. Любая случайная величина с множеством значений х: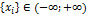 
, имеющая закон распределения f(x) и конечные ограниченные числовые характеристики 
. Тогда: Вероятность того, что модуль отклонения значений случайной величины х от её математического ожидания превышает или равно числу 
будет меньше или равно отношения 
к квадрату числа . 
Док-во: Пусть 
, изобразим на прямой случайных величин:
Из теории случайных величин 
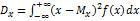
Оценим интеграл «в средне»: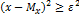 
-коридора, число которых с ростом N1>N уменьшается.
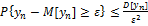. Воспользуемся представлением 
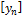через 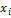. Обозначим 
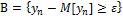и перейдём к 
. 
. 
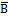. При фиксированном (малое положительное число) и при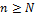 
и ограниченности 
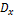будет выполняться условие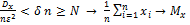 
Замечания:
1. Устанавливает связь между опытным определением средневзвешенного значения случайной величины х: 
и её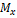 
.
2. Устанавливает, что опытным путём значение 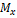случайной величины установить невозможно.
ожидание 
.
Зафиксируем n, найдём дисперсию 
Составим неравенство Чебышева для .
. 
приходим к неравенству, определяющему сходимость по вероятности .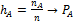
Замечания: 1. Тh Бернулли устанавливает связь между относительной частотой появления события А за n поставленных опытов и теоретической вероятности появления этого события в каждом опыте.
2. Положения теоремы Бернулли могут быть распространены и на другие вероятностные схемы.
Билет №5
Дата добавления: 2015-02-16; просмотров: 144 | Поможем написать вашу работу | Нарушение авторских прав |