Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Схема Бернулли. Формула Пуассона.

Схема Бернулли - схема последовательных, независимых испытаний в каждом опыте которой могут быть только 2 результата, которые образуют полную группу.

Пусть ставится n опытов 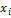, где i=1,2

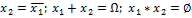
Опыт	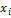Число наступлений	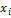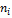Вероятность появления
	m	p
	n-m	q=1-p

Таким образом, необходимо установить наличие 2 результатов испытаний в целом. Определить условия проведения одного опыта. Выбрать 1 из результатов
при условии, что . Определить: событие А – искомое событие, n – число опытов, m – число опытов заканчивающихся событием , p=P() – вероятность в каждом опыте.

n, m	A	Условия Пуассона
p=P(), q=1-p

Т.е. . Формула Пуассона может быть получена из формулы Бернулли посредством предельного перехода и условия

Применяется при оценке вероятности P(A) в схеме Бернулли при условиях ; при оценке вероятностей редких событий

Билет №15.

1. Аксиомы теории вероятностей. Следствия к аксиомам.

AI: Вероятностью случайного события Р(А) – положительно-определённая на единичном интервале числовая мера, которая ставится в соответствие данному случайному событию.

Графика:

1.

2.

AII: Вероятность суммы 2 несовместных событий равна сумме их вероятностей.

Пусть А и В несовместны , тогда Р(А+В)=Р(А)+Р(В).

АIII: Вероятность суммы счётного множества попарно несовместных случайных событий равна сумме их вероятностей. 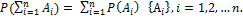Попарно несовместны .

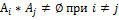I сл.: Сумма вероятностей противоположных событий равна 1.

II сл.: Вероятность суммы 2 произвольных событий можно вычислить: P(A+B)=P(A)+P(B) - P(A*B).

1. Все события попарно не совместны. 2. Сумма событий является достоверным событием.

.

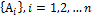
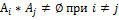Билет №16