Читайте также:
|
Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий: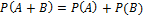 
.
Док-во: Введём обозначения: n – общее число возможных элементарных исходов испытания; 
- число исходов, благоприятствующих событию А; 
- число исходов, благоприятствующих событию В. Число элементарных исходов, благоприятствующих наступлению либо события А, либо события В равно 
Следовательно: 
, приняв во внимание, что 
.
Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.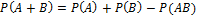 
Док-во: Поскольку события А и В, по условию, совместны, то событие А+В наступит, если наступит одно из следующих несовместных событий: 
. По теореме сложения вероятностей несовместных событий 
. Событие А произойдёт, если наступит одно из несовместных событий 
. По теореме сложения вероятностей несовместных событий 
Аналогично 
. Подставив (2), (3) в (1) получим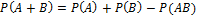
Теоремы умножения вероятностей. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении,
2. Функция распределения случайной величины – F(x) и её свойства.
Функция распределения случайной величины – функция действительного переменного x, 
определяющая вероятность того, что данная случайная величина принимает любые значения на интервале 
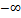до некоторого х малого, которое исключается из этого интервала, но совпадающая с аргументом формулы определения. 
Свойства 
:
1. Функция является положительно определённой на единичном интервале значений 
.
2. – неубывающая функция: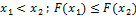 
.
3. Для дискретной x: 
4. 
5. 
Графика:
Для непрерывной величины
Для дискретной величины
Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.
n – полная группа, всевозможность.
вероятность следующего события: 
2. Функция распределения случайной величины – F(x) и её свойства.
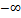Функция распределения случайной величины – функция действительного переменного x, определяющая вероятность того, что данная случайная величина принимает любые значения на интервале до некоторого х малого, которое исключается из этого интервала, но совпадающая с аргументом формулы определения.
Свойства :
1. Функция является положительно определённой на единичном интервале значений .
2. – неубывающая функция: .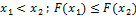
3. Для дискретной x:
4.
5.
Графика:
Для непрерывной величины
Для дискретной величины
что первое событие уже наступило: 
.
Док-во: По определению условной вероятности (условной вероятностью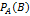 
называют вероятность события В, вычисленную в предположении, что событие А уже наступило), 
Вероятность совместного появления двух не зависимых событий равна произведению вероятностей этих событий.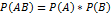 
Док-во: Событие В называют независимым от события А, если появление события А не изменит вероятности события В т. е. условная вероятность события В равна его безусловной вероятности: 
, тогда 
.
2. Функция плотности вероятности f(x) и её свойства.
Функцией плотности вероятностей случайной величины называется первая производная от функции распределения по её аргументу
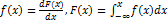
Свойства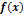 
:
1. 
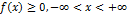
2. 
3. 
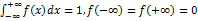
Графика:
1 – Функция мгновенного импульса.
Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.
n – полная группа, всевозможность.
Билет №9
Дата добавления: 2015-02-16; просмотров: 81 | Поможем написать вашу работу | Нарушение авторских прав |