
Читайте также:
|
Схема Бернулли - схема последовательных, независимых испытаний в каждом опыте которой могут быть только 2 результата, которые образуют полную группу.
Пусть ставится n опытов 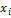 , где i=1,2
, где i=1,2
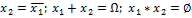
Опыт 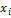
| Число наступлений 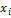 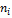
| Вероятность появления 
|

| m | p |

| n-m | q=1-p |

Таким образом, необходимо установить наличие 2 результатов испытаний в целом. Определить условия проведения одного опыта. Выбрать 1 из результатов
 при условии, что
при условии, что  . Определить: событие А – искомое событие, n – число опытов, m – число опытов заканчивающихся событием
. Определить: событие А – искомое событие, n – число опытов, m – число опытов заканчивающихся событием  , p=P(
, p=P( ) – вероятность
) – вероятность  в каждом опыте.
в каждом опыте.
| n, m | A | Вероятность одного сложного |
p=P( ), q=1-p ), q=1-p
|
события, состоящего в том, что в n испытаниях событие А наступит m раз и не наступит n-m раз по теореме умножению вероятностей независимых событий равна  . Таких сложных событий может быть столько, сколько можно составить сочетаний из n элементов по m элементов т.е.
. Таких сложных событий может быть столько, сколько можно составить сочетаний из n элементов по m элементов т.е.  . Так как эти сложные события несовместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равна сумме вероятностей всех возможных сложных событий, а так как вероятности всех этих событий одинаковы, то искомая вероятность равна вероятности одного сложного события, умноженная на их число:
. Так как эти сложные события несовместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равна сумме вероятностей всех возможных сложных событий, а так как вероятности всех этих событий одинаковы, то искомая вероятность равна вероятности одного сложного события, умноженная на их число:  .
.
Билет №14.
Дата добавления: 2015-02-16; просмотров: 97 | Поможем написать вашу работу | Нарушение авторских прав |