Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Нормальный закон распределения.

Нормальным законом распределения называют распределение вероятностей непрерывной случайной величины 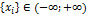, которое описывается плотностью

, где m - математическое ожидание случайной величины; σ² - дисперсия случайной величины, характеристика рассеяния значений случайной величины около математического ожидания; σ – среднеквадратическое отклонение СВ.

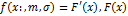- функция распределения случайной величины. Тогда - функция Лапласа.

Отсюда числовые характеристики нормального закона распределения:

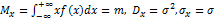
Свойства: 1. Нормальный закон – закон природы. 2. Нормальному закону будут подчиняться случайные величины составленные в виде 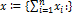при условии, что они не зависимы, и имеют различные законы распределения. (В частных случаях искомая х: может быть представлена, как сумма однородных случайных величин, имеющих одинаковый закон распределения, но слабо связанных друг с другом.)

3. Нормальный закон прост в определении характеристики и степени соответствия природному случайному явлению, в силу представления его параметров

. Составим неравенство Чебышева для .

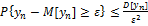. Воспользуемся представлением 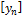через 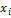. Обозначим 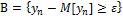и перейдём к 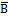. . . При фиксированном (малое положительное число) и при 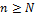и ограниченности 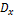будет выполняться условие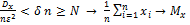

Замечания:

1. Устанавливает связь между опытным определением средневзвешенного значения случайной величины х: и её .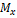

2. Устанавливает, что опытным путём значение 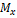случайной величины установить невозможно.

4. 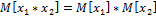, 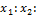- взаимно независимые.

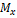любой случай величины является величиной не случайной, которая определяет некоторое единственное, устойчивое и средневзвешенное значение случайной величины на множестве её значений.

Геометрический смысл 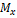определяется горизонтальной координатой центра тяжести фигуры под кривой вероятности.

2. Дисперсией любой случайной величины называется 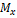квадрата разности значений величины и её .

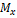1.

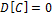
2.

3.

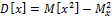
4. 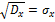– среднеквадратическое отклонение.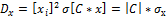

5.

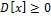
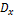любой случай величины является величиной не случайной, которая определяет меру разброса (отклонений) значений случайной величины и её математического ожидания.