Студопедия
Главная страница | Контакты | Случайная страница

АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатика
ИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханика
ОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторика
СоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансы
ХимияЧерчениеЭкологияЭкономикаЭлектроника

Локальная теорема Лапласа.

Читайте также:
  1. А)Определители 2-го,3-го и п-го порядков (определения и из св-ва). б)Теорема Лапласа о разложении определителя по элементам строки или столбца.
  2. Альтернативные правила принятия коллективных решений. Теорема Эрроу о невозможности.
  3. Билет 4. Теорема Гаусса для электростатики (в интегральной и дифференциальной форме).
  4. Вопрос №3 Поток вектора напряжённости. Теорема Гаусса для потока вектора напряжённости электрического поля.
  5. Дивергенция вектора. Теорема Гаусса в дифференциальной форме. Теорема Остроградского-Гаусса.
  6. Диэлектриктердегі электростатикалық өріс үшін Гаусс теоремасы.
  7. Единицы исторического процесса (этнос, страна, локальная цивилизация, человечество)
  8. Закон Био-Сарвала-Лапласа.
  9. Закон больших чисел. Первая теорема Чебышева.
  10. Й вопрос. Теорема Гауса для вектора напряженности эл. поля. Вычисление поля бесконечной однородно заряженной плоскости, двух равномерно заряженных плоскостей.

Если n – велико, а р – отлично от 0 и 1, то

где - функция Гаусса (функция табулирована, таблицу можно скачать на странице формул по теории вероятностей).

Интегральная теорема Лапласа.

Если n – велико, а р – отлично от 0 и 1, то

P(n; k1, k2) где - функция Лапласа (функция табулирована, таблицу можно скачать на странице формул по теории вероятностей).

Функции Гаусса и Лапласа обладают свойствами, которые необходимо знать при использовании таблиц значений этих функций:

а)

б) при больших 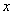верно .

Теоремы Лапласа дают удовлетворительное приближение при . Причем чем ближе значения к 0,5, тем точнее данные формулы. При маленьких или больших значениях вероятности (близких к 0 или 1) формула дает большую погрешность (по сравнению с исходной формулой Бернулли).

Закон больших чисел Бернулли и его выражение через функцию Лапласа.



Дата добавления: 2015-01-30; просмотров: 153 | Поможем написать вашу работу | Нарушение авторских прав


lektsii.net - Лекции.Нет - 2014-2025 год. (0.007 сек.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав