Читайте также:
|
В средне- и долгосрочных финансово-кредитных операциях, если проценты не выплачиваются сразу после их начисления, а присоединяются к сумме долга, применяют сложные проценты. База для начисления сложных процентов в отличие от простых не остается постоянной – она увеличивается с каждым шагом во времени. Абсолютная сумма начисляемых процентов возрастает, и процесс увеличения суммы долга происходит с ускорением. Наращение по сложным процентам можно представить как последовательное реинвестирование средств, вложенных под простые проценты на один период начисления (running period). Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, часто называют капитализацией процентов.
Найдем формулу для расчета наращенной суммы при условии, что проценты начисляются и капитализируются один раз в году (годовые проценты). Для этого применяется сложная ставка наращения. Для записи формулы наращения применим те же обозначения, что и в формуле наращения по простым процентам:
P — первоначальный размер долга (ссуды, кредита, капитала и т.д.),
S — наращенная сумма на конец срока ссуды,
п — срок, число лет наращения,
i — уровень годовой ставки процентов, представленный десятичной дробью.
Очевидно, что в конце первого года проценты равны величине Рi, а наращенная сумма составит 
. К концу второго года она достигнет величины 
В конце n-го года наращенная сумма будет равна
(4.1)
Проценты за этот же срок в целом таковы:
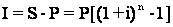(4.2)
Часть из них поучена за счет начисления процентов на проценты. Она составляет
Дата добавления: 2015-02-16; просмотров: 172 | Поможем написать вашу работу | Нарушение авторских прав |