Читайте также:
|
При разработке методов защиты информации в информационной среде следует учесть следующие важные факторы и условия:
♦ расширение областей использования компьютеров и увеличение темпа роста компьютерного парка (то есть проблема защиты информации должна решаться на уровне технических средств);
♦ высокая степень концентрации информации в центрах ее обработки и, как следствие, появление централизованных баз данных, предназначенных для коллективного пользования;
♦ расширение доступа пользователя к мировым информационным ресурсам (современные системы обработки данных могут обслуживать неограниченное число абонентов, удаленных на сотни и тысячи километров);
♦ усложнение программного обеспечения вычислительного процесса на компьютере.
При таких режимах работы в памяти компьютера одновременно могут находиться программы и массивы данных различных пользователей, что делает актуальным сохранение информации от нежелательных воздействий, ее физическую защиту.
К традиционным методам защиты от преднамеренных информационных угроз относятся: ограничение доступа к информации, шифрование (криптография) информации, контроль доступа к аппаратуре, законодательные меры.
Для защиты информации от случайных информационных угроз, например, в компьютерных системах, применяются средства повышения надежности аппаратуры:
· повышение надежности работы электронных и механических узлов и элементов;
· структурная избыточность — дублирование или утроение элементов, устройств, подсистем;
· функциональный контроль с диагностикой отказов, то есть обнаружение сбоев, неисправностей и программных ошибок и исключение их влияния на процесс обработки информации, а также указание места отказавшего элемента.
Основные понятия теории вероятностей. Случайные события. Вероятность.
· Достоверное событие. Событие называется достоверным, если оно обязательно произойдет при осуществлении определенной совокупности условий.
Обозначение: И (истина).
Пример: игральный кубик подбрасывается вверх, выпадет число от 1 до 6 (это достоверное событие).
· Невозможное событие. Событие, которое никогда не произойдет при определенной совокупности условий.
Обозначение: V
· Случайное событие. Может произойти или не произойти при выполнении определенной совокупности условий. Обозначение: A, B, C{\ldots}
События A и B будем называть несовместными, если появление события A исключает возможность появление события B. Иначе события будем называть совместными.
События называются равновозможными, если в результате испытаний ни одно из них не является более возможным, чем другое.
· Полная группа событий.
События будут образовывать полную группу, если в результате испытаний появится хотя бы одно из них.
Пример: Ai - i-е число на вершине грани кубика.
· Противоположные события - события, которые являются 2-мя возможными исходами одного испытания.
Обозначение: A, A
Примеры:
1. A - орел, A - решка; A
2. A - попадание в мишень, A - промах.
· Вероятностью случайного событи я p(A) называется отношение числа благоприятствующих данному событию исходов к общему числу всех равновозможных несовместных исходов, образующих полную группу.
Случайное событие — подмножество множества исходов случайного эксперимента; при многократном повторении случайного эксперимента частота наступления события служит оценкой его вероятности.
Случайное событие, которое никогда не реализуется в результате случайного эксперимента, называется невозможным и обозначается символом. Случайное событие, которое всегда реализуется в результате случайного эксперимента, называется достоверным и обозначается символом.
11. Вероятность появления события А при условии, что событие В произошло, называется условной вероятностью события А и вычисляется по формуле
В качестве разумного обоснования этого определения отметим, что при наступлении события B оно начинает играть роль достоверного события, поэтому надо потребовать, чтобы P(В|B) =1. Роль события A играет AB, поэтому P(A|B) должна быть пропорциональна P(АB).
(Из определения следует, что коэффициент пропорциональности равен 1/P(В))
События A и B называются независимыми, если P(A|B)=P(A).
Это означает: оттого, что произошло событие B, вероятность события A не изменилась.
С учетом определения условной вероятности, это определение сведется к следующему соотношению P(AB) = P(A)P(B). В этом соотношении нет необходимости требовать выполнения условия P(B)>0.Таким образом, приходим к окончательному определению.
События A и B называются независимыми, если P (AB) = P(A)P(B).
Последнее соотношение обычно и принимают за определение независимости двух событий.
Несколько событий называются независимыми в совокупности, если подобные соотношения выполняются для любого подмножества рассматриваемых событий. Так, например, события A,B,C, независимы в совокупности, если выполняются соотношения
P(ABC)=P(A)P(B)P(C), P(AB)=P(A)P(B), P(AC)=P(A)P(C), P(CB)=P(C)P(B).
12. Случайную величину называют непрерывной, если ее функция распределения есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.
Функцией распределения называют функцию, определяющую вероятность того, что случайная величина в результате испытания примет значение, меньшее.
Геометрически это равенство можно истолковать так: есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки.
Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.
Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями.
Число возможных значений дискретной случайной величины может быть конечным или бесконечным.
Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями.
Закон распределения дискретной случайной величины можно задать таблично, в виде формулы (аналитически) и графически.
Случайная величина, значения которой заполняют некоторый промежуток, называется непрерывной.
Из формулы P{Α ≤ X < Β}=F(Β)-F(Α)следует, что вероятность попадания случайной величины в заданный интервал определяется скоростью изменения функции распределения вероятностей на этом интервале. Скорость изменения непрерывной функции равна ее производной. Это позволяет ввести новую функцию для задания случайной величины. Рассмотрим снова вероятность попадания случайной величины в интервал [x,x+Δx]:
P{x≤X<x+Δx}=F(x+Δx)-F(x).
Пусть Х - непрерывная случайная величина. Тогда для малых значений Δx эта вероятность будет также достаточно малой. Поделим ее на Δx и перейдем к пределу при Δx →0:
limΔx →0(P{x≤X<x+Δx}/Δx)=limΔx →0(F(x+Δx)-F(x))/Δx).
Если это предел существует, то он равен производной от функции распределения F(x):
limΔx →0(F(x+Δx)-F(x))/Δx)=F'(x)=f(x).
Функция f(x) называется плотностью распределения вероятностей случайной величины Х. Из определения следует, что при малых значениях Δx справедливо равенство:
P{x≤X<x+Δx}≈f(x)*Δx.
13. Характеристики распределений случайной величины:
Математическим ожиданием непрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a,b], называется определенный интеграл.
При этом, конечно, предполагается, что несобственный интеграл сходится.
Дисперсией непрерывной случайной величины называется математическое ожидание квадрата ее отклонения.
Модой М0 дискретной случайной величины называется ее наиболее вероятное значение. Для непрерывной случайной величины мода – такое значение случайной величины, при которой плотность распределения имеет максимум.
Если многоугольник распределения для дискретной случайной величины или кривая распределения для непрерывной случайной величины имеет два или несколько максимумов, то такое распределение называется двухмодальным или многомодальным.
Если распределение имеет минимум, но не имеет максимума, то оно называется антимодальным.
Медианой MD случайной величины Х называется такое ее значение, относительно которого равновероятно получение большего или меньшего значения случайной величины.
Геометрически медиана – абсцисса точки, в которой площадь, ограниченная кривой распределения делится пополам.
Отметим, что если распределение одномодальное, то мода и медиана совпадают с математическим ожиданием.
14. Распределение Бернулли в теории вероятностей и математической статистике — дискретное распределение вероятностей, моделирующее случайный эксперимент произвольной природы, когда заранее известна вероятность успеха или неудачи.
Случайная величина имеет распределение Бернулли, если она принимает всего два значения: и с вероятностями и соответственно. Таким образом:
Принято говорить, что событие соответствует «успеху», а «неудаче». Эти названия условные, и в зависимости от конкретной задачи могут быть заменены на противоположные.
Биномиальное распределение в теории вероятностей — распределение количества «успехов» в последовательности из 
независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них постоянна и равна 
.
Пусть 
— конечная последовательность независимых случайных величин с распределением Бернулли, то есть
Построим случайную величину 
:
Тогда , число единиц (успехов) в последовательности 
, имеет биномиальное распределение с степенями свободы и вероятностью «успеха» . Пишем: 
. Её функция вероятности задаётся формулой:
где 
— биномиальный коэффициент.
Распределение Пуассона — вероятностное распределение дискретного типа, моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.
Распределение Пуассона играет ключевую роль в теории массового обслуживания.
Выберем фиксированное число 
и определим дискретное распределение, задаваемое следующей функцией вероятности:
, где
— 
обозначает факториал числа 
,
— 
основание натурального логарифма.
Тот факт, что случайная величина имеет распределение Пуассона с параметром 
, записывается: 
.
Непрерывное равномерное распределение — в теории вероятностей распределение, характеризующееся тем, что вероятность любого интервала зависит только от его длины.
Говорят, что случайная величина имеет непрерывное равномерное распределение на отрезке 
, где 
, если её плотность имеет вид:
Пишут: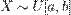 
. Иногда значения плотности в граничных точках и меняют на другие, например 0 или 
. Так как интеграл Лебега от плотности не зависит от поведения последней на множествах меры нуль, эти вариации не влияют на вычисления связанных с этим распределением вероятностей.
В теории вероятностей случайная величина имеет дискретное равномерное распределение, если она принимает конечное число значений с равными вероятностями.
Нормальное распределение, также называемое гауссовым распределением, гауссианой или распределением Гаусса — распределение вероятностей, которое задается функцией плотности распределения: 
где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ² — дисперсия.
Нормальное распределение играет важнейшую роль во многих областях знаний, особенно в статистической физике. Физическая величина, подверженная влиянию значительного числа независимых факторов, способных вносить с равной погрешностью положительные и отрицательные отклонения, вне зависимости от природы этих случайных факторов, часто подчиняется нормальному распределению, поэтому из всех распределений в природе чаще всего встречается нормальное (отсюда и произошло одно из названий этого распределения вероятностей).
Нормальное распределение зависит от двух параметров — смещения и масштаба, то есть является с математической точки зрения не одним распределением, а целым их семейством. Значения параметров соответствуют значениям среднего (математического ожидания) и разброса (стандартного отклонения).
Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1.
Дата добавления: 2015-01-30; просмотров: 212 | Поможем написать вашу работу | Нарушение авторских прав |