Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Анализ схемы во временной области

2.1. С помощью теоремы разложения получить выражения для импульсной и переходной характеристик и построить их графики друг под другом в одном масштабе по t.

и представить в виде суммы слагаемых вида - для вещественных полюсов и 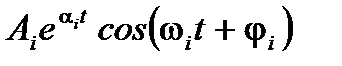- для комплексных полюсов, где – числа.

Исходя из того, что импульсной характеристикой является реакция на входной сигнал в виде функции Дирака, а переходной – реакция цепи на функцию Хэвисайда, найдем их.

Определим импульсную характеристику цепи:

Разложим выражение на сумму простых дробей, разложив знаменатель на множители:

Найдем производную знаменателя

Определим коэффициенты при вычетах функции в особых точках

Таким образом, имеем выражение для коэффициента передачи по напряжению в виде:

Теперь рассчитаем импульсную характеристику с помощью обратного преобразования Лапласа:

.

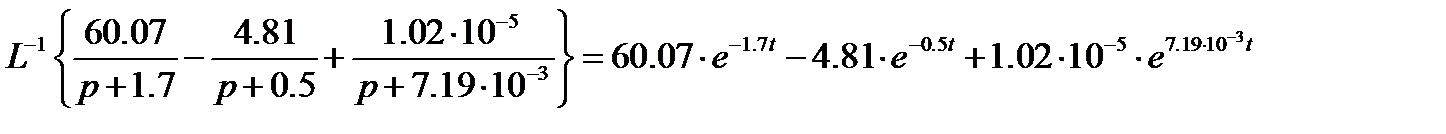Импульсная характеристика имеет вид:

Определим переходную характеристику цепи:

Найдем корни знаменателя выражения :

Разложим выражение 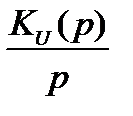на сумму простых дробей, разложив знаменатель на множители:

Найдем производную знаменателя

Определим коэффициенты при вычетах функции в особых точках

.

Таким образом, имеем выражение для 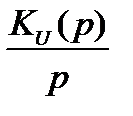в виде:

.

Теперь рассчитаем переходную характеристику с помощью обратного преобразования Лапласа:

.

Переходная характеристика имеет вид:

Построим графики импульсной (Рисунок 2.1) и переходной (Рисунок 2.2) характеристик:

1) Построим - (Рисунок 2.1).

Рисунок 2.1

2) Построим - (Рисунок 2.2).

Рисунок 2.2