
Т.Лагранжа:Пусть ф-ция f(x) определена на отрезке [a,b] и вып.след.условия: 1. f(x) 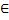 С [a,b] 2. f(x)
С [a,b] 2. f(x) 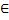 D [a,b]. Тогда
D [a,b]. Тогда 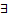 т с
т с 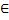 (a,b), что
(a,b), что 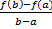 =f’(c). (Геометрич.смысл:если вып.условия, то
=f’(c). (Геометрич.смысл:если вып.условия, то 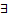 такая с,3 что кас-я,проведенная к дан.т. ф-ции f(x) будет ||хорде, кот.проходит с координатами ((a,f(a)),(b,f(b)). Т.Коши: Пусть f(x) и g(x) определ. на отр[a,b] и выполнено: 1. f(x) и g(x)
такая с,3 что кас-я,проведенная к дан.т. ф-ции f(x) будет ||хорде, кот.проходит с координатами ((a,f(a)),(b,f(b)). Т.Коши: Пусть f(x) и g(x) определ. на отр[a,b] и выполнено: 1. f(x) и g(x) 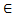 С[a,b] 2. f(x) и g(x)
С[a,b] 2. f(x) и g(x) 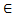 D(a,b) 3. g’(x)
D(a,b) 3. g’(x) 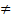 0
0 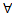 x
x 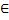 (a,b), тогда
(a,b), тогда 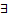 т.с
т.с 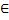 (a,b), что вып-ся:
(a,b), что вып-ся: 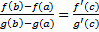
Билет 9.Признак монотонности функции. Теорема. Пусть f(x) опред.на интеревала (a,b) и 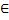 D в каждой точке этого инервала. Тогда, если f’(x)
D в каждой точке этого инервала. Тогда, если f’(x) 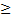 0(f’(x)
0(f’(x) 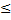 0)
0) 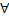 x
x 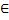 (a,b).то f(x) на итер-ле (a,b) не убывает(не возрастает)Док-во: пусть f(x)
(a,b).то f(x) на итер-ле (a,b) не убывает(не возрастает)Док-во: пусть f(x) 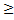 0
0 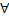 x
x 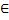 (a,b).требуется док-ть,что
(a,b).требуется док-ть,что 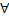 х1,х2
х1,х2 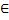 (a,b),x1
(a,b),x1 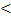 x2. Должно выпол-ся: f(x1)
x2. Должно выпол-ся: f(x1)  f(x2). Фикс.х1,х2∈(a,b), x1
f(x2). Фикс.х1,х2∈(a,b), x1 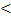 x2, по формуле Лагранжа: f(x2)-f(x1)=f’(c)(x2-x1). Где с
x2, по формуле Лагранжа: f(x2)-f(x1)=f’(c)(x2-x1). Где с 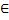 (х1,х2). f(x2)
(х1,х2). f(x2) 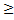 f(x1)=>f(x2)-f(x1)
f(x1)=>f(x2)-f(x1) 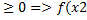 )
) 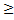 f(x1).
f(x1).
Точки локального экстремума. Опр.точка х0 наз лок.мин[макс], если 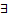 такая окр.т.х0(х0-
такая окр.т.х0(х0-  ,х0+
,х0+ 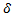 )=U
)=U  (x0), что
(x0), что 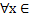 U
U  (x0) вып-ся:f(x0)<f(x) [f(x0)>f(x)].Опр.точки лок.мин и лок.макс.объединены в общее определение – точки экстремума.Теорема.Необходимое условие точек лок.экстремума). Пусть f(x) имеет в т х0 лок экстремум и
(x0) вып-ся:f(x0)<f(x) [f(x0)>f(x)].Опр.точки лок.мин и лок.макс.объединены в общее определение – точки экстремума.Теорема.Необходимое условие точек лок.экстремума). Пусть f(x) имеет в т х0 лок экстремум и 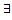 f’(x) в т х0(f(x)
f’(x) в т х0(f(x) 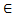 D(x0)).тогда f’(x0)=0. Док-во: следует из т.Ферма.дан.условие не явл.достаточным. Теорема(достат.условие точек лок.экстремума) пусть f(x)
D(x0)).тогда f’(x0)=0. Док-во: следует из т.Ферма.дан.условие не явл.достаточным. Теорема(достат.условие точек лок.экстремума) пусть f(x) 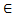 D(U
D(U  (x0)). Тогда если f’(x)>0 [f’(x)<0]
(x0)). Тогда если f’(x)>0 [f’(x)<0] 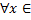 (x0-
(x0-  , x0) и f’(x)<0 [f’(x)>0
, x0) и f’(x)<0 [f’(x)>0 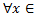 (x0, x0+
(x0, x0+ 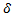 )], то х0- т.лок макс[мин].
)], то х0- т.лок макс[мин].
Дата добавления: 2015-04-11; просмотров: 75 | Поможем написать вашу работу | Нарушение авторских прав |