Читайте также:
|
Исходным показателем ДР является его уровень, показывающий на каком уровне происходит развитие. В зависимости от развития ДР встречаются:
1)устойчивые
2) не устойчивые.
Для того чтобы рассчитать коефициентвириации кое-нт вариации имеет вид:
V𝛿= 
*100
𝛿=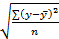 
Если Vсг менше 10 РД считается устойчивым.
10. К механ. приемам выравнивания дин. рядов относят способ укрупнения периодов и способ скользящей средней. Эти методы применяются для изучения неустойчивых дин. рядов, для выявления закономерности или тенденции развития явления.
Способ укрупнения периодов осуществляется п 3, 5 и 7 летним периодам. В данном случае периоды времени искомого ряда заменяются новыми укрупненными периодами, для которых исчисляются средние значения. Этот прием используется только для интервальных рядов динамики. Недостатком этого приема является то, что при его использовании не прослеживается процесс изменения явления внутри укрупненных интервалов.
Способ скользящей средней. При использовании данного метода анализируем скользящую среднюю, полученную путем последующего исключения начального члена интервала и замена его очередным. По укрупненным интервалам определяем среднюю из уровней, входящих в каждый интервал. Недостатки: в зависимости от периода осреднения мы теряем 1, 2, 3 и более уровней ряда; подсчитанные нами показатели не относятся ни к какому конкретному периоду времени.
11. Порядок выравнивания дин.ряда по способу наим. квадратов. Этапы, содержание. Суть выравнивания дин.ряда по сп.наим. квадратов заключается в замене эмпирических(фактич.) уровней дин.ряда такими теоретич. уровнями, кот. будут максимально приближены к эмпирическим и в то же время будут отражать основную тенденцию развития признаков. Матем. выражение денного признака: 
гдеyi– фактический уровень ряда, yt-теоретический. Эффективность выравнивания по способу наименьших квадратов в значительной мере зависит от правильности выбора математического уравнения, которое наиболее точно может проявить присущую ряду тенденцию.
Вначале строится график и на него наносятся фактич. уровни, затем подбирается соотв.уравнение типов выравнивающей линии. Для проведения аналит. выравнивания можно использовать следующие уравнения: уравнение прямой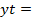 
a0+a1*t, уравнение параболы 2-го порядка: yt=a0+a1*t+a2*t2, уравнение параболы 3-го порядка: yt= a0+a1*t+a2*t2+a3*t3, и другим, где a0, a1, a2, a3 –неизвестные параметры, t-периоды времени. Затем для одно из уравнений составляется система нормальных уравнение, из этой системы находятся неизвестные параметры и подставляются в исходное уравнение. Затем определяются теоретические уровни и наносятся на график. После этого проводится дисперсионный анализ, в ходе которого рассчитывается коэффициент случайной вариации, если он меньше 50%, то мат.модель подобрана верно и имеет экон. смысл в расчетах, если больше-то необходимо подобрать другой тип выравн. линии.
12. Порядок выравнивания дин.ряда по способу наим. квадратов. Содержание параметров. Суть выравнивания дин.ряда по сп.наим.квадратов заключается в замене эмпирических(фактич.) уровней дин.ряда такими теоретич. уровнями,кот.будут максимально приближены к эмпирическим и в то же время будут отражать основную тенденцию развития признаков. Матем.выражение денного признака: гдеyi– фактический уровень ряда, yt-теоретический. Эффективность выравнивания по способу наименьших квадратов в значительной мере зависит от правильности выбора математического уравнения, которое наиболее точно может проявить присущую ряду тенденцию. Для проведения аналит.выравнивания можно использовать следующие уравнения: уравнение прямой 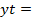a0+a1*t, уравнение параболы 2-го порядка: yt=a0+a1*t+a2*t2, уравнение параболы 3-го порядка: yt= a0+a1*t+a2*t2+a3*t3, и другим, где a0, a1, a2, a3 –неизвестные параметры, t-периоды времени.
13. Аналитическое выравнивание по методу наим. квадратов. Дисперс.анализ. Суть выравнивания дин.ряда по сп.наим.квадратов заключается в замене эмпирических(фактич.) уровней дин.ряда такими теоретич. уровнями,кот.будут максимально приближены к эмпирическим и в то же время будут отражать основную тенденцию развития признаков. Матем.выражение денного признака: гдеyi– фактический уровень ряда, yt-теоретический. Эффективность выравнивания по способу наименьших квадратов в значительной мере зависит от правильности выбора математического уравнения, которое наиболее точно может проявить присущую ряду тенденцию. Для проведения аналит.выравнивания можно использовать следующие уравнения: уравнение прямой 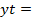a0+a1*t, уравнение параболы 2-го порядка: yt=a0+a1*t+a2*t2, уравнение параболы 3-го порядка: yt= a0+a1*t+a2*t2+a3*t3, и другим, где a0, a1, a2, a3 –неизвестные параметры, t-периоды времени.
Чтобы определить, какое из уравнений больше подходит для аналитического выравнивания проведем дисперсионный анализ в динамическом ряду. Дисперсионный анализ позволяет разделить действия постоянных и случайных факторов, которые оказывают влияние на изучаемый признак. Все факторы, которые вызывают вариацию признаков можно поделить на группы: - постоянно действующие; - случайные, разово действующие.Суть дисперсионного анализа заключается в следующем: рассчитывается столько дисперсий остаточных, сколько подобрало типов выравнивающих линий. Та линия, которой соответствует наименьшее значение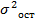 
, лучше отражает сложившуюся тенденцию развития. Рассчитаем дисперсию остаточную:
, 
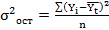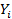– фактические уровни динамического ряда, 
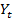– теоретические уровни динамического ряда, рассчитанные по уравнению прямой; 
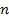– количество уровней. По наименьшему значению проводится весь дальнейший анализ. Рассчитывается общая дисперсия:
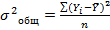. Рассчитывается дисперсия факторная: 
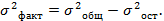Рассчитаем коэффициенты случайной вариации отражающей долю случайно действующих факторов
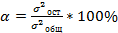. Рассчитаем коэффициент детерминации, отражающий факторы, формирующие основную тенденцию развития признака: 
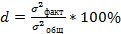.Если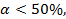 
то модель подобрана верно.
Дата добавления: 2015-04-12; просмотров: 168 | Поможем написать вашу работу | Нарушение авторских прав |