Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Оценим качество уравнения регрессии с помощью коэффициента детерминации.

Нескорректированный коэффициент множественной детерминации оценивает долю вариации результата за счет представленных в уравнении факторов в общей вариации результата. Здесь эта доля составляет 94,2% и указывает на весьма тесную связь факторов с результатом.

Скорректированный коэффициент множественной детерминации определяет тесноту связи с учетом степени свободы общей и остаточной дисперсии.

Оба коэффициента указывают на весьма высокую (более 90%) детерминированность результата у в модели.

3. Используя пошаговую множественную регрессию, построим модель формирования прибыли от реализации за счёт значимых факторов.

Рассчитаем линейные коэффициенты частной корреляции, используя инструмент Анализа данных КОРРЕЛЯЦИЯ (рис.3)

Рис.3. Результат применения инструмента КОРРЕЛЯЦИЯ

Значения коэффициентов парной корреляции указывают на связь между признаками.

Так как между факторными признаками x₁ и x₂ существует эффект мультиколлинеарности (коэффициент корреляции между ними 0,9488>0,8), то для построения модели выбираем признаки x₁, x₃ и x₄ (x₂ отбрасываем, так как коэффициент корреляции между x₂ и Y меньше, чем между x₁ и Y 0,9535<0,9557).

Как мы видим по ранжиру наименьшая связь между признаками у и х₃ и признаками у и х₄ . Исключим данные признаки из уравнения. Рассмотрим однофакторное линейное уравнение (рис.4):

Рис.4. Результат применения инструмента РЕГРЕССИЯ и КОРРЕЛЯЦИЯ для парного уравнения

По результатам вычислений составим уравнение регрессии вида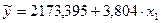

Рис. 5. Двухфакторная модель

Рис. 6. Трехфакторная модель включения фактора х₃ после х₁ и х₂

Рис. 7. Трехфакторная модель включения фактора х₃ после х₁ и х₂

На основе частных F -критериев Фишера оценим целесообразность включения фактора х₂ в модель после того, как в нее включен фактор х₁ по формуле (используя данные рис.5):

, следовательно, приходим к выводу, что включение х₂ после х₁ статистически значим и оправдан.

По результатам вычислений составим уравнение множественной регрессии:

Оценим целесообразность включения фактора х₃ в модель после того, как в нее включены факторы х₁ и х₂ по формуле (используя данные рис.6):

, следовательно, приходим к выводу, что включение х₃ после х₁ и х₂ оказался бесполезным.

Оценим целесообразность включения фактора х₃ в модель после того, как в нее включены факторы х₁ и х₂ по формуле (используя данные рис.6):

, следовательно, приходим к выводу, что включение х₄ после х₁ и х₂ оказался бесполезным.

Следовательно, вполне возможно ограничится построением двухфакторного уравнения