Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Основные положения

α -распад — распад атомных ядер, сопровождающийся испуска­нием α-частиц (ядер ⁴Не).

Часть изотопов могут самопроизвольно испускать α-частицы (ис­пытывать α-распад), т. е. являются α-радиоактивными. Подавляю­щее большинство α-радиоактивных изотопов (более 200) расположе­но в периодической системе в области тяжелых ядер (Z > 83). Это обусловлено тем, что α-распад связан с кулоновским отталкиванием, которое растет по мере увеличения размеров ядер быстрее (как Z²), чем ядерные силы притяжения, которые растут линейно с ростом массового числа А.

Ядро α-радиоактивно, если выполнено условие, являющееся след­ствием закона сохранения энергии

М (А, Z) > М(А - 4, Z - 2) + М _α, (1)

где М(А, Z) и М(А—4, Z—2) — массы исходного и конечного ядер со­ответственно, М _α — масса α-частицы. При этом в результате распада конечное ядро и α-частица приобретают суммарную кинетическую энергию

Q_α = [М(A, Z) – М(А - 4, Z - 2) - М _α]с², (2)

которая называется энергией α-распада. Ядра могут испытывать α-распад также на возбужденные состояния конечных ядер и из воз­бужденных состояний начальных ядер. Поэтому соотношение (2.13) для энергии а-распада можно обобщить следующим образом:

Q_α = [М(A, Z) – М(А - 4, Z - 2) - М_α]с²+ (3)

где и — энергии возбуждения начального и конечного ядер соответственно. α-частицы, возникающие в результате распада воз­бужденных состояний ядер, получили название длиннопробежных. Для большинства ядер с А > 190 и для многих ядер с 150 < А < 190 условие (12) выполняется. Однако, далеко не все они считаются α-радиоактивными. Дело в том, что современные эксперименталь­ные возможности не позволяют обнаружить α-радиоактивность для нуклидов с периодом полураспада большим, чем 10¹⁶ лет. Кроме то­го, часть «потенциально» α-радиоактивных ядер испытывают также β-распад, который конкурирует с α-распадом.

Основную часть энергии α-распада (около 98 %) уносят α-частицы. Используя законы сохранения энергии и импульса, для ки­нетической энергии α-частицы Т_а можно получить соотношение

(4)

Периоды полураспада известных α-радиоактивных нуклидов ва­рьируются от 0,298 мкс для ²¹²Ро до (2…5) · 10¹⁵ лет для ¹⁴²Се, ¹⁴⁴Ne, ¹⁷⁴Hf. Энергия α-частиц, испускаемых тяжелыми ядрами из основ­ных состояний, составляет 4…9 МэВ, ядрами редкоземельных эле­ментов — 2…4,5 МэВ.

Важным свойством α-распада является то, что при небольшом изменении энергии α-частиц периоды полураспада изменяются на много порядков. Так у ²³²Th Q_α = 4.08 МэВ, Т _1/2 = 1.41·10¹⁰ лет, а у ²¹⁸Th Q_a = 9.85 МэВ, Т _1/2 = 10 мкс. Изменению энергии в 2 раза соответствует изменение периода полураспада на 24 порядка.

Для четно-четных изотопов элемента зависимость периода полу­распада от энергии α-распада хорошо описывается эмпирическим законом Гейгера-Неттола

lg Т_1/2=A + B/(Q_α) ^1/2,

где А и В — константы, слабо зависящие от Z. С учетом заряда до­чернего ядра Z связь между периодом полураспада Т_1/2 и энергией α-распада Q _α может быть представлено в виде

, (5)

где Т _1/2 в с, Q_a в МэВ. Периоды полураспада для нечетно-четных, четно-нечетных и нечетно-нечетных ядер в 2…10³ раз больше, чем для четно-четных ядер с данными Z и Q_a.

При прохождении через вещество тяжелая заряженная частица теряет кинетическую энергию на ионизацию и возбуждение атомов вещества. Эти потери и определяют пробег частицы. Вероятность ионизации атомов среды при энергиях в несколько МэВ примерно в 10³ раз больше вероятности ядерного взаимодействия. Величина ионизационных потерь, обусловленных кулоновским взаимодействи­ем пролетающей частицы заряда z с электронами вещества, опреде­ляется главным образом ее зарядом, скоростью v и плотностью элек­тронов в веществе п_е. В нерелятивистском случае удельные иониза­ционные потери тяжелой заряженной частицы массы М т_е, (т_е — масса электрона), определяются зависимостью

(6)

Поэтому с уменьшением скорости удельные потери заряженной частицы в веществе возрастают.

В одном акте ионизации в воздухе α-частица теряет около 35 эВ. Т. е. если начальная кинетическая энергия α-частицы равна 4 МэВ, то она полностью затормозится в результате 4·10⁶/35 ≈ 10⁵ актов ионизации.

Взаимодействие α-частиц с ядрами вещества в основном сводит­ся к кулоновскому рассеянию на малые углы. Таким образом, при движении в среде заряженные частицы с указанной энергией будут постепенно тормозиться на длине пробега R. Траектория движения тяжелой заряженной частицы в среде правило прямолинейна, а про­бег определяется интегралом

(7)

Пробег R измеряется в сантиметрах или в массовой толщине ρ (г/см²).

Рис. 1: Определения пробега R_a и экстраполированного пробега R_e α-частиц.

Пробег R_a определяется как толщина слоя вещества, при про­хождении которого поглощается половина частиц (см. рис. 1). Ино­гда также используется понятие экстраполированного пробега R_e. Он определяется с помощью экстраполяции по касательной к кри­вой пробега из точки, соответствующей поглощению половины ча­стиц. Как видно из рис. 1 пробеги имеют разброс значений про­бега (страгглинг), описываемый функцией Гаусса. Он обусловлен в частности статистическими флуктуациями ионизационных потерь. Действительно, если среднее число ионов, образуемое α-частицей на длине ее пробега, равно N, то среднеквадратичное отклонение от этого числа, будет . Кроме того, при прохождении через вещество α-частица может испытать перезарядку, превращаясь в однозаряд­ный ион гелия (⁴Не⁺) или в атом гелия (⁴Не). Разный заряд частицы на всем пути вызывает дополнительные флуктуации в ионизации и, следовательно, в пробеге.

Удельные ионизационные потери энергии в веществе со сложным химическим составом можно рассчитать по формуле

, (8)

где М — молекулярный вес соединения, N _i — количество атомов сорта г с атомным весом A_i в молекуле, (dE/dp)_i — удельные потери для данного простого вещества.

При расчетах длина пробега альфа-частицы R определяется из экспериментальных формул. Для воздуха при 0^оС и 760 мм рт. Ст. величина пробега альфа-частицы с энергией 3…10 MeV может быть определена по формуле Гейгера с точностью до 5%:

где Е_a - энергия альфа-частицы, MeV.

Длина пробега альфа-частиц в других средах может быть определена по формуле Брэгга:

или по формуле Глессена:

где Е - энергия альфа-частицы, MeV; А - атомный вес; z - порядковый номер; ρ - плотность вещества. Величину пробега альфа-частицы в любой среде R _ср можно определить по величине пробега в воздухе R, если известна относительная тормозная способность S, рассчитанная на один атом

,

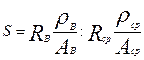где ρ_В=1,293·10^-3 г/см³, R _В = 3,7 см.