Читайте также:
|
Пусть задана сложная функция 
.
Теорема. Если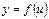 
и 
- дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу и умноженной на производную промежуточного аргумента по независимой переменной 
, т.е.
.
□ Дадим независимой переменной х приращение Δ х ≠0. Тогда функция u= φ (x) и у=f (u) соответственно получат приращения Δ u и Δ y.
Предположим, что Δ u ≠0. Тогда в силу дифференцируемости функции у=f (u) можно записать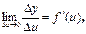 
где - f ′(u) величина не зависящая от Δ u.
На основании теоремы о связи бесконечно малых величин с пределами функций 
где 
- бесконечно малая величина при Δ u → 0, откуда 
Это равенство будет справедливо и при Δ u = 0, если полагать, что α(∆ u =0)=0 (т.е. доопределить таким образом функцию α(∆ u) при ∆ u =0).
Разделив обе части последнего равенства на Δ х ≠0, получим 
Так как по условию функция у=φ (х) дифференцируема, то она непрерывна в точке х, следовательно, при Δ х → 0 Δ u → 0 и α(∆ u) → 0.
Поэтому, переходя к пределу при Δ х → 0 в последнем соотношении, получаем 
■
Дата добавления: 2015-09-11; просмотров: 21 | Поможем написать вашу работу | Нарушение авторских прав |