Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Признаки возрастания и убывания функции.

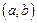Определение. Функция называется возрастающей на интервале , если для любых точек из этого интервала при выполнении условия выполняется неравенство (большему значению аргумента соответствует большее значение функции).

Определение. Аналогично, функция называется убывающей на интервале , если для любых точек из этого интервала при выполнении условия выполняется неравенство (большему значению аргумента соответствует меньшее значение функции).

Возрастающие на интервале и убывающие на интервале функции называются монотонными на интервале .

Знание производной дифференцируемой функции позволяет находить интервалы ее монотонности.

Теорема (достаточное условие возрастания функции). Если производная дифференцируемой на интервале 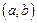функции положительна на интервале 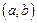, то функция 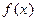монотонно возрастает на этом интервале.

Доказательство. Зафиксируем любые точки на интервале такие, что .

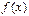Тогда по следствию из теоремы Лагранжа , где . По условию на всем интервале , то есть , следовательно, . Таким образом, действительно возрастает на 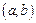, что и требовалось доказать.

Теорема (достаточное условие убывания функции). Если производная дифференцируемой на интервале 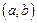функции 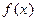отрицательна на интервале , то функция монотонно убывает на этом интервале.

Геометрический смысл этих теорем состоит в том, что на интервалах убывания функции касательные к графику функции образуют с осью тупые углы, а на интервалах возрастания – острые (см. рис. 4).

Алгоритм нахождения интервалов монотонности функции .

1. Найти .
2. Найти нули производной.
3. На числовой оси отметить область определения , нули производной и те точки, где производная не существует.
4. На каждом из полученных интервалов определить знак производной .
5. Сделать вывод о возрастании или убывании функции на каждом интервале.

Пример. Пусть . Найдем . Далее, при и при . Имеем, что при и при , и при . Это значит, что при и при функция возрастает, а при функция убывает.