
Определение. Под знакопеременным рядом  понимается ряд, в котором любой член может быть как положительным, так и отрицательным.
понимается ряд, в котором любой член может быть как положительным, так и отрицательным.
Теорема (достаточный признак сходимости знакопеременного ряда). Если ряд, составленный из абсолютных величин членов знакопеременного ряда  сходится, то сходится и исходный ряд.
сходится, то сходится и исходный ряд.
Определение. Ряд называется абсолютно сходящимся, если ряд, составленный из абсолютных величин его членов, сходится.
Определение. Ряд называется условно сходящимся, если сам ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится.
Пример. Исследовать на абсолютную сходимость ряд 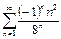 .
.
Решение. Составим ряд из абсолютных величин членов данного ряда:  . Применим признак Даламбера:
. Применим признак Даламбера: 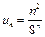 ,
,  ,
, 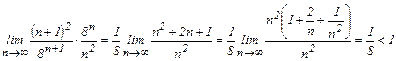 , т.е. ряд, составленный из модулей членов исходного ряда, сходится.
, т.е. ряд, составленный из модулей членов исходного ряда, сходится.
Следовательно, знакочередующийся ряд 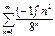 сходится абсолютно.
сходится абсолютно.
48. Условия разложения функций в степенной ряд. Ряд Маклорена. Разложение в ряд Маклорена функции у=е x (вывод). Интервал сходимости полученного ряда
Определение. Ряды, членами которых являются функции, называются функциональными, в частности, если членами ряда являются степенные функции, то такие ряды называются степенными:  (14.1)
(14.1)
где числа  - коэффициенты ряда.
- коэффициенты ряда.
Определение. Совокупность тех значений  , при которых степенной ряд (14.1) сходится, называется областью сходимости степенного ряда.
, при которых степенной ряд (14.1) сходится, называется областью сходимости степенного ряда.
Пример. Найти область сходимости степенного ряда  . Решение. Этот ряд можно рассматривать как геометрический ряд со знаменателем
. Решение. Этот ряд можно рассматривать как геометрический ряд со знаменателем  , который сходится при
, который сходится при 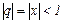 . Откуда область сходимости есть интервал
. Откуда область сходимости есть интервал 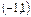 .
.
Теорема Абеля. 1) Если степенной ряд сходится при значении  (отличном от нуля), то он сходится и, притом абсолютно, при всех значениях
(отличном от нуля), то он сходится и, притом абсолютно, при всех значениях  таких, что
таких, что 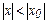 . 2) Если степенной ряд расходится при
. 2) Если степенной ряд расходится при 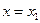 , то он расходится при значениях
, то он расходится при значениях  таких, что
таких, что  .
.
Следствие. Из теоремы Абеля следует, что существует такое число  , что при
, что при 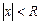 ряд сходится, а при
ряд сходится, а при 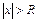 - расходится.
- расходится.

| Число 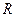 получило название радиуса сходимости, а интервал получило название радиуса сходимости, а интервал  - интервал сходимости степенного ряда (рис. 14.1).
На концах отрезка - интервал сходимости степенного ряда (рис. 14.1).
На концах отрезка 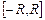 ряд может как сходиться, так и расходиться. ряд может как сходиться, так и расходиться.
|
Пример. Найти радиус сходимости степенного ряда (14.1), если все коэффициенты 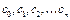 (по крайней мере с некоторого номера
(по крайней мере с некоторого номера 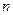 отличны от нуля).
отличны от нуля).
Решение. По признаку Даламбера ряд сходится, если 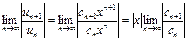 будет меньше 1. Т.е.
будет меньше 1. Т.е. 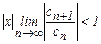 или
или 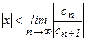 . Если этот предел существует, то он и является радиусом сходимости
. Если этот предел существует, то он и является радиусом сходимости 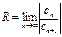 . (14.2)
. (14.2)
Пример. Найти область сходимости степенного ряда:  . Решение. Радиус сходимости определяется по формуле (14.2)
. Решение. Радиус сходимости определяется по формуле (14.2) 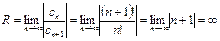 , т.е. область сходимости
, т.е. область сходимости 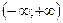 .
.
Дата добавления: 2015-09-11; просмотров: 81 | Поможем написать вашу работу | Нарушение авторских прав |