Читайте также:
|
Дифференциальное уравнение 1-го порядка называется однородным, если оно может быть представлено в виде
, (12.6)
где 
- некоторая функция от 
(одной переменной).
Понятие однородного дифференциального уравнения тесно связано с однородными функциями. Функция 
называется однородной степени 
(по переменным 
и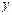 
), если для произвольного числа 
выполняется равенство:
.
Пример. Выяснить является ли однородной функция: 
.
Решение. Т.к. 
, то данная функция однородная степени 2.
Однородные дифференциальные решаются с помощью подстановки 
, которая приводит уравнение (12.6) к уравнению с разделяющимися переменными.
Решение: Пусть 
, тогда 
, 
откуда получим: 
Пример. Решить уравнение 
.
Решение. 
Замена: 
, 
. 
- уравнение с разделяющимися переменными.
Разделим переменные и выполним почленное интегрирование 
. 
,
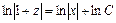- общее решение.
Дата добавления: 2015-09-11; просмотров: 82 | Поможем написать вашу работу | Нарушение авторских прав |