Читайте также:
|
Теорема. Пусть функция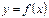 
непрерывна на отрезке 
и 
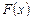- любая первообразная для 
на . Тогда определенный интеграл от функции на отрезке равен приращению первообразной 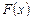на этом отрезке, т.е.
.
Значение определённого интеграла равно разности значений любой первообразной от подынтегральной функции, взятых при верхнем и нижнем пределах интеграла.
Другими словами, Значение определённого интеграла равно приращению любой первообразной от подынтегральной функции на интервале интегрирования.
Формула Ньютона-Лейбница позволяет находить определённый интеграл, обходя суммирование, при помощи первообразных функций.
Несобственные интегралы с бесконечными пределами интегрирования. Интеграл Пуассона (без доказательства).
Дата добавления: 2015-09-11; просмотров: 73 | Поможем написать вашу работу | Нарушение авторских прав |