
Читайте также:
|
Определение:
Последовательность называется финально постоянной, если $ AО R и $ N, что для всех n>N xn = A.
Свойство 1: Пределы конечного числа функции равен сумме пределов, если пределы функции существуют.
1)lim(f(x)+g(x)) (при x→a, x→∞) = lim f(x) (при x→a, x→∞)+ +lim g(x) (при x→a, x→∞);
2) lim f(x)=b1 (при x→a, x→∞)
lim (f(x)+g(x)) (при x→a, x→∞)=b1+b2
lim g(x)=b2 (при x→a, x→∞)
По первому свойству б.м. (обратная теорема) имеем что: f(x)=b1+α(x)
g(x)=b2+β(x)
Следовательно f(x)+g(x)=b1+b2+α(x)+ β(x); γ(x)= α(x)+ β(x)
f(x)+g(x)=b1+b2+γ(x)=> по I свойству бесконечно малых(прямая теорема), что lim (f(x)+g(x)) (при x→a, x→∞)=b1+b2 – бесконечно мало.
lim (sin2x+cos2x) (при x→∞)≠lim sin2x(при x→∞)+lim cos2x(при x→∞)[Таких не существует].
Свойство 2:
Предел произведения конечного числа сомножителей равен произведению пределов этих сомножителей, если последние существуют.
 Доказательство для n=2. Пусть
Доказательство для n=2. Пусть  ;
;  , тогда u1=а 1 +a1, u2=а 2 +α2, где α1→0, α2→0 при х→х0, и u1·u2=(а 1+ а 2 ) · ( α1+α2 ) = а 1 а 2+ α1а2 + α2а1 +α2α1, где а1а2=const, α1а2→0, α2 а 1 →0, α2α1 →0 при х→х0. По теореме о связи функции с ее пределом будем иметь, что
, тогда u1=а 1 +a1, u2=а 2 +α2, где α1→0, α2→0 при х→х0, и u1·u2=(а 1+ а 2 ) · ( α1+α2 ) = а 1 а 2+ α1а2 + α2а1 +α2α1, где а1а2=const, α1а2→0, α2 а 1 →0, α2α1 →0 при х→х0. По теореме о связи функции с ее пределом будем иметь, что 
Следствие. Постоянный множитель можно выносить за знак предела:

Свойство 3: Предел частного двух функций равен частному пределов этих функций при условии, что предел знаменателя не равен нулю:
 .
.
Свойство 4: Если между соответствующими значениями функций u(x), v(x), ω(x) выполняются неравенства u(x)≤v(x)≤ω(x), при этом u(x), ω(x) при х→х0 стремятся к одному и тому же пределу а, то функция v(x) при х→х0 стремится к этому же пределу.
Свойство 5: Если функция у=f(x) принимает неотрицательные значения, то есть f(x)≥0, и имеет предел равный а, то этот предел тоже неотрицателен, то есть а ≥ 0.
Свойство 6: Если между соответствующими значениями функций u(x), v(x), имеющих предел при х→х0, выполняется неравенство u(x)≤v(x), то 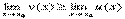 .
.
Дата добавления: 2015-09-10; просмотров: 99 | Поможем написать вашу работу | Нарушение авторских прав |