
|
Читайте также: |
Предположим, что нам даны две плоскости, отнесенные к прямоугольным координатам  и
и  .
.
 Рассмотрим в этих плоскостях две замкнутые области
Рассмотрим в этих плоскостях две замкнутые области  и
и  с контурами
с контурами 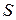 и
и  соответственно.
соответственно.
Пусть в области  задана система функций
задана система функций
 .
.
Будем считать, что  и
и  являются однозначными функциями
являются однозначными функциями  и
и 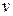 и более того, система уравнений однозначно разрешима относительно
и более того, система уравнений однозначно разрешима относительно  и
и 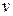 , т.е.
, т.е.  и
и 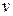 являются однозначными функциями
являются однозначными функциями  и
и  .
.
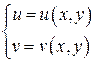 .
.
Тем самым между областями  и
и  устанавливается взаимно-однозначное соответствие. Говорят, что формулы осуществляют преобразование области
устанавливается взаимно-однозначное соответствие. Говорят, что формулы осуществляют преобразование области  в область
в область  ; а формулы дают обратное преобразование. При этом, точкам контура
; а формулы дают обратное преобразование. При этом, точкам контура  соответствуют точки контура
соответствуют точки контура 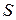 и наоборот.
и наоборот.
Предположим, что функции имеют в  непрерывные частные производные первого порядка. Тогда функциональный определитель
непрерывные частные производные первого порядка. Тогда функциональный определитель  (якобиан) является непрерывной функцией двух переменных
(якобиан) является непрерывной функцией двух переменных  и
и 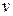 в области
в области  .
.
Будем считать, что этот определитель не равен нулю и, следовательно, сохраняет постоянный знак в силу непрерывности.
Задание пары значений  и
и 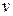 в области
в области  в то же самое время однозначно определяет некоторую точку в области
в то же самое время однозначно определяет некоторую точку в области  ; в силу этого числа (
; в силу этого числа ( и
и 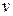 ) (помимо
) (помимо  и
и  ) можно считать координатами точек в области
) можно считать координатами точек в области  .
.
Определение. Кривую, составленную из точек области  , у которых одна из координат
, у которых одна из координат  или
или 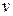 сохраняет постоянное значение, называют координатной линией.
сохраняет постоянное значение, называют координатной линией.
Если в положить  , получим параметрическое представление координатной линии
, получим параметрическое представление координатной линии  . (Роль параметра играет
. (Роль параметра играет  .)
.)
Неявное уравнение той же линии можно получить, полагая во втором уравнении системы  :
:  .
.
В связи с тем, что координатные линии на плоскости  вообще говоря, будут кривыми, то числа
вообще говоря, будут кривыми, то числа  и
и 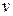 , характеризующие положение точки на плоскости, называются криволинейными координатами точки.
, характеризующие положение точки на плоскости, называются криволинейными координатами точки.
Придавая 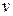 различные значения, получим на плоскости
различные значения, получим на плоскости  семейство координатных линий. Фиксируя значение
семейство координатных линий. Фиксируя значение  , получим другое семейство координатных линий. При наличии взаимнооднозначного соответствия между рассматриваемыми областями, различные линии одного и того же семейства не пересекаются, и через любую точку области
, получим другое семейство координатных линий. При наличии взаимнооднозначного соответствия между рассматриваемыми областями, различные линии одного и того же семейства не пересекаются, и через любую точку области  проходит по одной линии из каждого семейства.
проходит по одной линии из каждого семейства.
Вся сетка координатных линий на плоскости  является изображением сетки прямых
является изображением сетки прямых  ;
;  на плоскости
на плоскости  .
.
Дата добавления: 2015-09-10; просмотров: 89 | Поможем написать вашу работу | Нарушение авторских прав |