Читайте также:
|
Пусть функция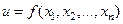 
задана уравнением 
, связывающим значение функции и аргументов, и неразрешённым относительно функции 
. В этом случае говорят, что функция задана неявно. Не всякое уравнение определяет некоторую функцию.
Например, уравнение 
не имеет действительных решений и не задает никакой функции.
Теорема “О существовании неявно заданной функции”. Если в некоторой окрестности точки 
функция 
имеет непрерывные частные производные 
и 
, кроме того частная производная 
в точке 
не обращается в 0 (
), тогда уравнение в некоторой окрестности точки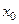 
определяет , как неявно заданную однозначную функцию своих аргументов 
, и частные производные функции 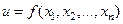в точке 
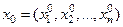вычисляются по формулам:
, 
, …, 
.
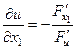Частные случаи:
1) Неявно заданная функция одного аргумента 
: 
.
2) Неявно заданная функция двух аргументов 
:
.
Пример.
Найти частные производные неявно заданной функции по аргументам 
и 
:
Имеем: 
, 
.
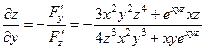Дата добавления: 2015-09-10; просмотров: 93 | Поможем написать вашу работу | Нарушение авторских прав |