Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Магнитное поле бесконечно длинного соленоида

Соленоид - это проволочная катушка цилиндрической формы. Его можно представить себе как множество сложенных в стопку круговых витков с током. Силовые линии магнитного поля, создаваемого электри­ческим током в соленоиде, показаны на рис. 6.6. Как видно из этого рисунка, внутри соленоида силовые линии почти прямые. Чем длин­нее соленоид, т.е. чем больше его длина по сравнению с его радиусом, тем меньше кривизна силовых линий внутри соленоида. В таком случае вектор В магнитной индукции поля внутри соленоида будет направлен параллельно его оси. Причем так, что его направление будет связано с направлением тока в соленоиде правилом правого винта. Направим ось х вдоль оси соленоида. При этом проекция вектора магнитной индукции на ось х будет равна его модулю, а все другие его проекции будут равны нулю:

B_x =B, B_y =B_z =0.

Подставим эти проекции вектора В в уравнение (6.12). Получим

¶B/¶x = 0

Из этого равенства вытекает, что внутри соленоида вектор магнитной индукции не только сохраняет свое направление, но его модуль здесь всюду одинаков. Таким образом, приходим к выводу, что внутри длин­ного соленоида магнитное поле является однородным.

.

Рис. 6.6. Магнитное поле соленоида

Найдем модуль вектора магнитной индукции поля внутри соленоида при помощи теоремы (6.8) о циркуляции этого вектора. В качестве кон­тура С, по которому будем вычислять циркуляцию вектора магнитной индукции, выберем ломанную линию, изображенную пунктиром на рис. 6.6. Отрезок этой линии длиной l находится внутри соленоида и совпа­дает с одной из силовых линий магнитного поля. Две перпендикулярные этому отрезку прямые начинаются на его концах и уходят в бесконеч­ность. Во всех точках этих прямых вектор магнитной индукции или перпендикулярен им (внутри соленоида), или равен нулю (вне соленои­да). Поэтому скалярное произведение Вdl в этих точках равно нулю. Таким образом, циркуляция магнитной индукции по рассматриваемому контуру С будет равна интегралу по отрезку силовой линии длиной l. С учетом того, что модуль вектора магнитной индукции есть постоянная величина будем иметь

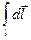= =B =B l

Пусть число витков соленоида, охватываемых контуром С, равно N. При этом сумма токов, охватываемых контуром, будет равна NI, где I - сила тока в одном витке соленоида. Теорема (6.8) приводит к равенству

Вl = μ_o NI,

из которого найдем магнитную индукцию поля в соленоиде:

В = μ_o nI

(6.14)

где n=N/l

n-число витков, приходящихся на единицу длины соленоида.