
Читайте также:
|
Рассмотрим магнитное поле постоянного тока I, текущего по проводу в форме окружности С радиуса а. Применим закон Био - Савара -Лапласа для определения магнитной индукции в центре кругового тока.
На рис.6.2 изображены вектор dl, характеризующий произвольный малый участок проводника с током, и вектор R, соединяющий этот участок с точкой О, в которой требуется определить магнитную индукцию В. По определению векторного произведения из формулы (6.1) следует, что вектор dB магнитной индукции поля, создаваемого рассматриваемым участком тока, перпендикулярен и вектору dl, и вектору R. Таким образом, начало вектора dB находится в точке О, а сам вектор перпендикулярен плоскости контура С.



|
Рис. 6.2.К расчету магнитного поля кругового тока
Так как векторы dl и R образуют прямой угол, модуль вектора dB согласно формуле (6.3) будет
dB = μoIdl/ (4p a 2)
Векторы dB магнитной индукции полей, создаваемых различными участками контура в точке О, совпадают по направлению. В таком случае их векторная сумма будет представлять собой вектор В, который имеет то же направление. При этом модуль этого вектора будет равен
сумме модулей векторов dB:
B = 

В =  = μoI/ (4p a 2)
= μoI/ (4p a 2) 
Интеграл от dl
 =2p a
=2p a
Таким образом, придем к следующей формуле для магнитной индукции поля, создаваемого круговым током в центре окружности:
B=μoI/ (2a) (6.5)
Модуль рт вектора магнитного момента кругового тока равен произведению силы тока на площадь круга:
рт =I p a 2
Использоя это соотношение, выражение (6.5) можно записать так:
B=μoрт / (2p a 3) (6.6)
В центре кругового витка с током вектор магнитной индукции направлен так же, как вектор магнитного момента рт. При этом справедливо соотношение
B =μo рт / (2p a 3) (6.7)
Отметим, что направление вектора магнитной индукции в центре кругового тока связано с направлением электрического тока правилом правого винта.
Линиив пространстве, к которым вектор В в любой точке является касательным, называются силовыми линиями магнитного поля. На рис. 6.3 изображены силовые линии магнитного поля кругового тока.

Рис. 6.3. Силовые линии магнитного поля кругового тока
§ 1. Магнитное поле. Закон Ампера
Между проводниками с током существует взаимодействие, называемое магнитным. Осуществляется взаимодействие посредством магнитного поля: один проводник с током создает в пространстве магнитное поле  , другой проводник находится в этом поле. На элемент тока I
, другой проводник находится в этом поле. На элемент тока I  в магнитном поле действует сила Ампера
в магнитном поле действует сила Ампера
 . (1)
. (1)
На проводник с током конечной длины действует сила
 (2)
(2)
Вектор  называется вектором индукции магнитного поля.
называется вектором индукции магнитного поля.
§ 2. Закон Био-Савара-Лапласа. Принцип суперпозиции для вектора 
 Элемент тока I
Элемент тока I  проводника с током создает в т.А с радиусом вектором
проводника с током создает в т.А с радиусом вектором 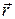 магнитное поле
магнитное поле  , вычисляемое в соответствии с законом Био-Савара-Лапласа по формуле
, вычисляемое в соответствии с законом Био-Савара-Лапласа по формуле
 . (1)
. (1)
Все элементы тока, из которых состоит проводник с током, создают поле
 (2)
(2)
что соответствует принципу суперпозиции для магнитного поля

 (3)
(3)
§ 3. Применение принципа суперпозиции для вычисления индукции магнитного поля 
1. Магнитное поле прямого тока I.
 Все d
Все d  всех элементов тока I
всех элементов тока I  направлены одинаково, поэтому
направлены одинаково, поэтому
 ; B =
; B =  .
.


 . (1)
. (1)
Поле  направлено по касательной к окружности в т.А.
направлено по касательной к окружности в т.А.
2. Магнитное поле на оси кругового тока.
 dB z = dB ·cosa B z =
dB z = dB ·cosa B z =  =
= 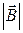 .
.

 :
:

r 2 = R 2 + Z2; 
 . (2)
. (2)
Поле  направлено по оси Z.
направлено по оси Z.
3. Вычислив с помощью принципа суперпозиции поле во всем пространстве, можно найти силу  взаимодействия токов по формуле (1.2).
взаимодействия токов по формуле (1.2).
§ 4. Взаимодействие параллельных токов. Единица силы тока 1 А



 . (1)
. (1)
По проводнику идет ток силой 1 А, если сила F 1 взаимодействия на единицу длины проводника равна 2.10-7 Н при расстоянии между проводниками 1 м.
§ 5. Закон полного тока для магнитного поля в вакууме

Рассмотрим плоский контур в виде окружности в плоскости, перпендикулярной прямолинейному проводнику с током I c центром О. Вычислим для этого контура


 (1)
(1)
Равенство (1) справедливо для произвольных формы контура L и охватываемого им тока I. Если через поверхность, натянутую на контур L течет несколько токов, то в (1) под током I подразумевается алгебраическая сумма токов, т.е.
 (2)
(2)
Если ток I распределен по поверхности S плотностью  то
то  и
и
 (3)
(3)
Выражения (1) – (3) носят название закона полного тока для магнитного поля в вакууме, записанного в интегральной форме.
Если выполнить математические преобразования вида

устремляя размеры контура к нулю, то получим дифференциальную форму закона полного тока
 (4)
(4)
или
 (4¢)
(4¢)
§ 6. Применение закона полного тока для вычисления магнитного поля
1. Поле прямого тока  .
.
2. Поле тороида 
3. Поле соленоида 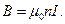
Дата добавления: 2015-09-11; просмотров: 186 | Поможем написать вашу работу | Нарушение авторских прав |