Читайте также:
|
Непосредственной причиной появления тока в контуре являются силы, заставляющие заряды-носители тока перемещаться по проводнику. Действие этих сил, приводящее к упорядоченному движению зарядов, характеризуется электродвижущей силой (ЭДС). По определению ЭДС
есть циркуляция вектора Е напряженности поля сторонних сил:
e = 
(8.3)
Напомним, что сторонней называется любая сила, действующая на подвижный электрический заряд, кроме силы, обусловленной действием постоянного электрического поля.
Проанализировав результаты опытов Фарадея, Максвелл установил, что причиной появления индукционного тока является электродвижущая сила индукции, которая равна с обратным знаком производной по времени от магнитного потока (8.1):
- ЭДС индукции в замкнутом контуре.
|
(8.4)
Запишем уравнение (8.4) подробнее, подставив в него интегралы (8.1) и (8.3):
(8.5)
Предложенное Максвеллом уравнение (8.5) описывает открытый Фарадеем закон электромагнитной индукции. Условились, что направле ние обхода контура С, задаваемое вектором dl, связано с направлением нормали п к поверхности S, натянутой на этот контур, правилом правого винта. Имея в виду это условие, из уравнения (8.5) можно найти
направление вектора напряженности Е, который согласно закону Ома
j = s Е
определяет направление тока в контуре С. Таким образом, в уравнении (8.5) правило Ленца учитывается автоматически.
Убедимся в справедливости уравнения (8.4) на следующем примере. Рассмотрим прямоугольный плоский проводящий контур (рис. 8.3,а), одна из сторон MN которого перемещается со скоростью v параллельно
самой себе без нарушения контакта между проводами. Внешнее маг нитное поле однородно, а его индукция В направлена перпендикулярно
плоскости контура. В качестве поверхности S, по которой будем вычислять поток вектора В, удобно выбрать плоскость, натянутую на рассматриваемый контур. Вектор нормали п направим по полю: n || В.
Так как поле однородно и модуль вектора В постоянен, магнитный поток будет равен произведению модуля магнитной индукции на площадь контура:
Ф = 
= 
= 
= BS (8.7)
■
Площадь контура S = Ba x(t). Таким образом, приходим к формуле
Рис. 8.3. К вычислению электродвижущей силы индукции
Теперь найдем электродвижущую силу, действующую в контуре. Для этого нужно установить природу сторонних сил и найти эти силы. Пусть стержень MN, образующий подвижную сторону контура, изготовлен из металла и носителями тока в нем являются электроны. Движение электронов вместе со стержнем со скоростью v приводит к появлению силы Лоренца
F =-e[ vB ],
которая действует на электрон вдоль стержня (рис. 8.3, б) и создает индукционный ток в контуре. Это и есть в данном случае сторонняя сила. Ее напряженность
E = [ vB ], (8.8)
Если магнитное поле постоянно, то сторонние силы возникают только в подвижных частях контура. В этом случае электродвижущая сила
e =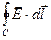 
= 
Направление вектора dl определяется выбором направления вектора нормали п и связано с ним правилом правого винта (рис. 8.3, а). Нетрудно видеть, что векторы dl и Е коллинеарны и направлены в разные стороны. При этом их скалярное произведение будет
Еdl =-Edl. (8.9)
e = = = - 
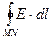= -vB 
= -vBa. (8.10)
Из формулы (8.7) получим
dФ/dt = Bav (8.11)
Сравнивая выражения (8.10) и (8.11), приходим к равенству (8.4).
Согласно правилу Ленца индукционный ток препятствует причине, его вызывающей. Каким образом это происходит в рассматриваемом примере? Так как по проводнику MN течет электрический ток, на него действует силу Ампера
F = I[ lB ], (8.12)
где вектор l направлен по току. По закону Ома (8.6) направление тока
совпадает с направлением вектора напряженности Е. Поэтому согласно формуле (8.12) силу Ампера будет направлена противоположно вектору скорости v. Движение проводника MN является причиной возникниве-ния в контуре индукционного тока. Этот ток направлен так, что сила Ампера препятствует движению проводника.
Рассмотрим теперь случай, когда проводящий контур С неподвижен, а магнитное поле изменяется со временем. Из уравнения Максвелла (8.5) следует, что при этом в контуре также действует электродвижущая сила. Какова в этом случае природа сторонних сил? Так как контур неподвижен, силы Лоренца не могут в таком случае играть роль сторонних сил
Максвелл предположил, что меняющееся со временем магнитное поле создает в пространстве электрическое поле, которое и заставляет носители тока перемещаться в проводнике. Причем это поле создается вне зависимости от того, присутствуют ли в пространстве подвижные заряды
или проводники. Из уравнения (8.5) видно, что циркуляция вектора Е напряженности этого поля не равна нулю, т.е. в отличие от постоянного электрического поля это поле не является потенциальным. Силовые линии электрического поля, которое создается изменяющимся магнитным полем, всегда замкнуты и поэтому такое поле называют вихревым.
При помощи теоремы Стокса уравнение (8.5) можно преобразовать к виду:
(1)
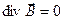(2)
Здесь вектор 
- вектор напряжённости электрического поля,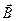 
- вектор индукции магнитного поля.
Уравнения образуют Первую пару уравнений Максвелла:
Первое из этих уравнений связывает значение с изменениями вектора 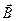во времени и является по существу выражением закона электромагнитной индукции. Оно показывает, что источником вихревого поля вектора является меняющееся со временем вихревое магнитное поле. Второе уравнение указывает на отсутствие источников магнитного поля, т.е. магнитных зарядов, как в вакууме, так и в намагниченном веществе.
Выводя формулу (1), Максвелл предположил, что изменяющегося со временем магнитное поле обусловливает появление в пространстве поля 
, независимо от присутствия в пространстве проволочного контура. Наличие контура лишь позволяет обнаружить по возникновению в нем индукционного тока существование в соответствующих точках пространства электрического поля.
Рассмотрим случай электромагнитной индукции, когда проволочный контур, в котором индуцируется ток, неподвижен, а изменения магнитного потока обусловлены изменениями магнитного поля. Возникновение индукционного тока свидетельствует о том, что изменения магнитного поля вызывают появление в контуре сторонних сил, действующих на носители тока. Эти сторонние силы не связаны ни с химическими, ни с тепловыми процессами в проводе; они также не могут быть магнитными силами, потому что такие силы над зарядами работы не совершают. Остаётся заключить, что индукционный ток обусловлен возникающим в проводе электрическим полем. Обозначим напряжённость этого поля (это обозначение является вспомогательным так же как и 
). Электродвижущая сила равна циркуляции вектора по данному контуру:
(1.1)
Подстановка в формулу
выражения (1.1) для 
и выражения 
для 
приводит к соотношению
(интеграл в правой части берётся по произвольной поверхности, опирающейся на контур). Поскольку контур и поверхность неподвижны, операции дифференцирования по времени и по поверхности можно поменять местами:
(1.2)
В связи с тем, что вектор 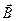зависит, вообще говоря, как от времени, так и от координат, то можно написать под знаком интеграла символ частной производной по времени (интеграл является функцией только времени).
Левую часть равенства (1.2) преобразуем по теореме Стокса. В результате получится:
.
Ввиду произвольности выбора поверхности интегрирования должно выполняться равенство
.
Ротор поля в каждой точке пространства равен взятой с обратным знаком производной по времени от вектора .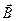
Это поле , порождающееся изменением магнитного поля, существенно отличается от порождаемого электрическими зарядами электрического поля . Электростатическое поле потенциально, его линии начинаются и заканчиваются на зарядах. Ротор вектора в любой точке равен нулю:
=0.
Согласно (1.2) ротор вектора отличен от нуля. Следовательно, поле так же, как и магнитное является вихревым. Линии напряжённости замкнуты.
Таким образом, электрическое поле может быть как потенциальным () так и вихревым (). В общем случае электрическое поле слагается из этих двух полей.
уравнение (1) также носит имя Максвелла и выражает открытый им закон, согласно которому изменяющееся магнитное поле порождает вихревое электрическое поле. Если магнитное поле постоянно, получим известное уравнение электростатики
=0.
rot E =0
Рассмотрим проволочную катушку, состоящую из N витков. Когда катушка находится в изменяющемся магнитном поле, в каждом витке возникает ЭДС. Так как витки соединены последовательно, электродвижущая сила в катушке будет равна сумме электродвижущих сил, действующих в каждом витке:
e = åNi eI = -åNi dФ/dt = -dåNi Ф/dt
где Фi - магнитный поток через виток под номером i; ei - возникающая в этом витке ЭДС индукции. Величину
y = åNi Ф
называют потокосцеплением, или полным магнитным потоком. Если магнитные потоки через все витки одинаковы, то потоков
y = N Ф.
Используя определение (8.14), электродвижущую силу, возникающую в катушке, можно записать так:
|
Пусть в произвольном замкнутом контуре протекает электрический
ток силой I. Этот ток создает в пространстве магнитное поле, индукция
которого в силу закона Био - Савара - Лапласа пропорциональна силе тока I. Согласно определениям (8.1) и (8.14), полный магнитный поток также будет
пропорционален силе тока
y = LI (8.16)
Коэффициент пропорциональности L называют индуктивностью контура. Индуктивность зависит от формы и размеров контура и от магнитных свойств среды, окружающей контур. Если сила тока изменяется со временем или изменяется индуктивность контура, потокосцепление будет иметь отличную от нуля производную по времени (y¢ ¹ 0). При этом в контуре будет действовать электродвижущая сила, которая обусловлена изменением тока в этом же контуре. Это явление называют самоиндукцией. В том случае, когда индуктивность контура не изменяется со временем, формулы (8.15) и (8.16) приводят к следующему выражению для электродвижущей силы самоиндукции:
- ЭДС самоиндукции. (8.17)
Единица измерения индуктивности в СИ называется генри (Г):
[L] = Г = Т м2/ А = Ом с.
Дата добавления: 2015-09-11; просмотров: 109 | Поможем написать вашу работу | Нарушение авторских прав |