
Читайте также:
|
Пусть пространство внутри соленоида заполнено веществом, магнитная проницаемость которого равна μ. Ток проводимости, текущий в соленоиде, относится к категории свободных токов. Его сила I считается заданной величиной. В веществе циркулируют молекулярные токи, плотность которых неизвестна.
Силовые линии магнитного поля, создаваемого электрическим током
в соленоиде, показаны на рис. 6.6. Для нахождения модуля вектора Я воспользуемся теоремой о циркуляции (7.7). В качестве контура интегрирования С выберем прямоугольный контур, изображенный пунктирной линией на рис. 6.6. Циркуляция вектора H по этому контуру будет равна криволинейному интегралу по отрезку силовой линии, который является частью контура С:
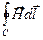 = Hl
= Hl
Сумма сил токов проводимости, охватываемых контуром С, равна силе
тока I в одном витке, умноженной на число витков на отрезке l:
å I* = Inl
В силу теоремы (7.7) о циркуляции вектора напряженности магнитного поля будем иметь
Н=пI. (7.17)
Из этой формулы видно, что модуль вектора Н внутри длинного соленоида всюду одинаков. Учитывая также неизменность его направлений, можно утверждать, что магнитное поле внутри соленоида однородно.
Причем направление вектора Н внутри соленоида связано с направлением тока в соленоиде правилом правого винта.
Если контур С располагается вне соленоида, то он не охватывает ни одного витка с током. При этом
å I* =0
В этом случае теорема о циркуляции вектора Н дает следующий результат:
Н =0,
т.е. магнитное поле вне бесконечно длинного соленоида отсутствует.
Магнитную индукцию внутри соленоида можно найти по формуле (7.12), если известна магнитная проницаемость /л среды, которая заполняет его внутренность:
В =μnI (7.18)
Дата добавления: 2015-09-11; просмотров: 126 | Поможем написать вашу работу | Нарушение авторских прав |