
Читайте также:
|
Интегральные уравнения (6.9) и (7.9) выражают основные законы постоянного магнитного поля в веществе. Запишем систему этих уравнений:
 =0
=0

|
(7.15)
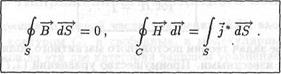
|
Этим интегральным уравнениям соответствуют дифференциальные уравнения
| (7.16) |
div В = 0, rot H = j*
Уравнения, выражающие собой законы постоянного магнитного поля, следует дополнить материальным уравнением
В =μ H,
.
Функции В = В (r) и Н = H (r), являющиеся решением этой системы, описывают постоянное магнитное поле в веществе создаваемое свободными токами заданной плотности.
В тех случаях, когда линии электрического тока расположены в пространстве симметрично, можно заранее предугадать, какими должны быть семейства силовых линий магнитного поля. В таких случаях, зная
направление вектора H напряженности магнитного поля, его модуль H можно найти по теореме (7.9) о циркуляции этого вектора или из уравнения (7.10). Затем следует найти вектор В. После этого можно найти вектор намагниченности.
Задача 1. Пространство между плоскостями х = -а u х = а заполнено однородным веществом, магнитная проницаемость которого равна μ. В веществе протекает свободный электрический ток плотности
j {0, 0, j}, где j - постоянная. Найти напряженность H и магнитную индукцию В поля, создаваемого этим током.
Задача 2. Бесконечный цилиндр радиуса R изготовлен из однородного вещества, магнитная проницаемость которого равна μ. По объему цилиндра вдоль его оси идет свободный электрический ток постоянной плотности j. Найти выражения для векторов H и В.
Задача 3. Бесконечный цилиндр радиуса R заряжен равномерно по объему с плотностью заряда д. Цилиндр вращается вокруг своей оси с угловой скоростью w. Найти вектор магнитного момента части цилиндра длиной l и векторы напряженности и магнитной индукции. Магнитная проницаемость вещества, из которого изготовлен цилиндр, равна μ ,.
Дата добавления: 2015-09-11; просмотров: 123 | Поможем написать вашу работу | Нарушение авторских прав |
|