
|
Читайте также: |
Ориентация на прямой: определяется заданием не 0го вектора, направление данного вектора положительное, противоположное- отрицательное. Ориентация на плоскости: опред заданием упорядоченной пары линейно-независимых векторов. 2 неколлинеарных вектора задают положит. ориентацию если кротчайший угол поворота осущ против часовой стрелки, и отрицат. в обратном случае. Ориентация в пространстве: опред. заданием упорядоченной тройки неколлинеарных векторов. (Правая и левая тройки)  -правая 3ка, если кратчайший поворот между
-правая 3ка, если кратчайший поворот между 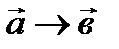 виден из конца вектора
виден из конца вектора  против часовой стрелки. Опр: Векторным произведением векторов
против часовой стрелки. Опр: Векторным произведением векторов  наз. вектор
наз. вектор  , такой что: 1) Этот вектор перпендикулярен векторам
, такой что: 1) Этот вектор перпендикулярен векторам  2)
2)  -правая 3ка. 3)
-правая 3ка. 3)  Обозначается
Обозначается  . Если
. Если 
Свойства векторного произв: 1)  2)
2)  Док-во: направление: а) если
Док-во: направление: а) если




2)  3)
3)  Длина:
Длина: 



1) 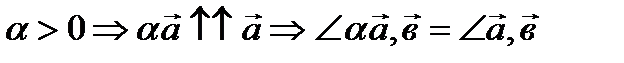 2)
2)  3)
3)  Док-во: (вспомогат) Рассмтр
Док-во: (вспомогат) Рассмтр 

 Докажем, что
Докажем, что  ,
, 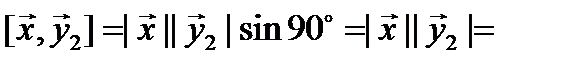 Рассмотрим:
Рассмотрим: 

 Для доказательства дост:
Для доказательства дост: 

 Рассмотрим
Рассмотрим 
 вектор
вектор  получается из
получается из 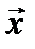 поворотом на 90 град против часовой стрелки в плоскости
поворотом на 90 град против часовой стрелки в плоскости 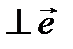
 так как
так как  умножаем
умножаем 
 4)
4)  или а, в коллинаерны 5)
или а, в коллинаерны 5)  площади паралел-ма построенного на векторах а и в
площади паралел-ма построенного на векторах а и в  Выражение векторного произведения через координаты векторов в ортонормиров базисе.
Выражение векторного произведения через координаты векторов в ортонормиров базисе.  -базис
-базис




.  пусть в базисе
пусть в базисе  имеют координаты
имеют координаты 





 Теорема: в ортонормированном базисе
Теорема: в ортонормированном базисе 
Дата добавления: 2015-09-11; просмотров: 99 | Поможем написать вашу работу | Нарушение авторских прав |