Однополостный: 
- сечение однополосного гиперболойда 2-мя плоскостями
- сечение однополосного гиперболойда
-однополосный вращение
1) yOz: 
2) xOz: 
3) 
; а) 
эллипс с полуосями 
(чем |h| больше, тем полуоси больше); 
Прямолинейной образующей поверхности назовем прямую целиком лежащую на поверхности. Теорема: через каждую точку однополостного гипербалоида проходят две прямолинейных образующих. Д-во: 
; 
; 
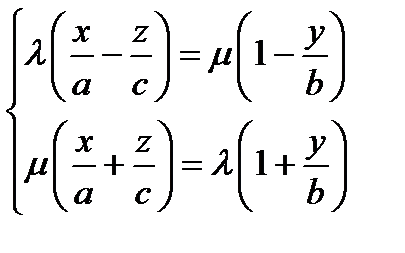- ур-ия двух пл-стей (первая прямая); 
- вторая прямая
Вращение гиперболы 
вокруг Oz:
Двухполостный: 
- Сечения двуполостного гиперболоида плоскостью xOz
-двуполосный гиперболоид
1) yOz: 
- гипербола с действ осью z и мнимой у
2) xOz: 
- гипербола с действ осью z и мнимой х
3) ; 
а) эллипс с полуосями 
(чем |h| больше, тем полуоси больше);
б) |h|<|c| - пустое множество
в) |h|=|c| - 2 точки (0,0,c) и (0,0,-c)
Вращение гиперболы 
вокруг Oz: 
-двуполосный вращение
Конус.
1) 
- две прямые
2) 
- две прямые
3) ; 
а) эллипс с полуосями 
(чем |h| больше, тем полуоси больше);
б) h=0 – 1 точка (0,0,0) – вершина
ЗЫ Конус – асимптотическая поверхность для гипербалоидОВ
Дата добавления: 2015-09-11; просмотров: 119 | Поможем написать вашу работу | Нарушение авторских прав |