
Читайте также:
|
Анализ чувствительности модели определяет оценку влияния колебаний значений входных переменных на отклики (выходные переменные) модели. Необходимо установить, при каком разбросе входных данных сохраняется справедливость основных выводов, сделанных по результатам моделирования.
Под анализом чувствительности понимаем определение чувствительности наших окончательных результатов моделирования к изменению используемых значений параметров. Анализ означает, как меняется выходная переменная Y при небольших изменениях различных параметров модели или ее входов X.
Простота проведения анализа чувствительности в имитационном моделировании – одно из преимуществ этого метода. Оценка чувствительности является исключительно важной процедурой и подготовительным этапом перед планированием имитационного эксперимента.
Дело в том, что величины параметров систематически варьируются в некоторых представляющих интерес пределах (Хmin – Хmax) и наблюдается влияние этих вариаций на характеристики системы (Ymin –
Ymax). Если при незначительных изменениях величин некоторых параметров результаты меняются очень сильно, то это – основание для затраты большого количества времени и средств с целью получения более точных оценок. И наоборот, если конечные результаты при изменении величин параметров в широких пределах не изменяются, то дальнейшее экспериментирование в этом направлении бесполезно и неоправданно.
Поэтому очень важно определить степень чувствительности результатов относительно выбранных для исследования величин – параметров. Исследование чувствительности является предварительной процедурой перед планированием эксперимента и позволяет определить стратегию планирования экспериментов на имитационной модели. Этой информации бывает достаточно для ранжирования компонент вектора параметров модели Х по значению чувствительности вектора отклика модели. Если модель оказывается малочувствительной по какой-либо q -й компоненте вектора параметров модели Хq, то зачастую не включают в план имитационного эксперимента изменение Хq, чем достигается экономия ресурса времени моделирования.
Анализ чувствительности поможет также внести коррективы в разрабатываемую модель – упростить, например, перейти от использования закона распределения к использованию среднего значения переменной, а некоторые подсистемы вообще отбросить (или процессы не детализировать). И наоборот, анализ чувствительности может показать, какие части модели было бы полезно разработать более детально.
Чувствительность имитационной модели представляется величиной минимального приращения выбранного критерия качества, вычисляемого по статистикам моделирования, при последовательном варьировании параметров моделирования на всем диапазоне их изменения.
Методика (процедура) оценки чувствительности [33]:
По каждому фактору Х определяется интервал изменения (minXq', maxXq). Остальные компоненты вектора Х не изменяются и соответствуют центральной точке. Проводят пару модельных экспериментов и получают отклики модели (min Y, max Y соответственно). Для оценки чувствительности используют абсолютные значения или относительные. В последнем случае вычисляют приращение вектора параметров

Итак, чувствительность модели по q - компоненте вектора параметров
Х определяют парой значений ( ).
).
Все рассмотренные процедуры в комплексе дают необходимую информационную базу обеспечения доверия к разработанной имитационной модели и перехода к следующим этапам работы с моделью.
Тактическое планирование имитационного эксперимента.
Процедуры верификации и валидации собственно имитационной модели и её программного кода требуют проведения широкого спектра тестовых имитационных экспериментов согласно сценариям, разработанным в процессе как тактического, так и стратегического планирования.
Стратегическое планирование (подробно рассматривается в следующей лекции) направлено на решение задач анализа чувствительности имитационной модели и определение комбинации оптимизирующих исследуемую систему параметров.
Тактическое планирование позволяет определиться с условиями проведения каждого прогона в рамках составленного плана эксперимента и связано с вопросами эффективности и определением способов проведения испытаний (прогонов), намеченных планом экспериментов.
Тактическое планирование направлено на решение проблемы точностного оценивания имитационных моделей и связано с тем, что в условиях стохастической модели, чтобы достигнуть заданной точности результатов экспериментов стремятся повторять реализации (проводить многочисленные прогоны). Время на серию машинных прогонов сложного модельного эксперимента может быть большим, а выделенное на эксперимент машинное время ограничивается имеющимися временными и машинными ресурсами. Поэтому необходимо стремиться к получению максимальной информации с помощью небольшого числа прогонов.
Основное противоречие – между точностью результатов и ограничением на ресурс (затратами на машинное время и на проведение серии экспериментов). На практике ищется компромисс. Выше мы обсуждали, что экспериментатор должен не только получить данные, но и оценить их точность, т.е. степень доверия к тем выводам, которые будут сделаны на основе этих результатов. Поэтому он стремится увеличить продолжительность прогона или число прогонов (размер выборки), т.к. от этого зависит точность результатов.
Основные вопросы (задачи) тактического планирования, которые решаются в связи с этим:
• Определение продолжительности имитационного прогона или требуемого числа повторений каждого прогона (размера выборки), обеспечивающего заданную точность результатов моделирования;
• Определение длительности переходного режима (анализ установившегося состояния), задание начальных условий (начального состояния).
Здесь решаются также такие задачи:
- выбор корректного шага моделирования, поскольку именно от шага моделирования зависит точность воспроизведения в имитационной модели имеющих место в реальной системе цепочек событий;
- контроль повторяемости результатов;
- установление правил остановки;
- уменьшении дисперсии выходов (используются специальные методы понижения дисперсии);
- снижение погрешности имитации, обусловленной наличием в имитационной модели генераторов псевдослучайных чисел;
- и многие другие.
Рассмотрим основные задачи тактического планирования.
Определение необходимого числа прогонов.
Основные методы организации прогонов: повторные прогоны, метод подинтервалов (прогоны делятся на группы, вычисляется среднее). Чтобы сделать статистический анализ по всей последовательности моделируемого случайного процесса, либо повторяют имитацию несколько раз (метод повторных прогонов), либо имитируют более продолжительное время (метод удлиненных прогонов).
Основные методы задания продолжительности имитационного прогона:
• Часто задается момент времени завершения моделирования;
• Метод, управляющий размером выборки (применяются правила автоматической остановки):
- задание определенного числа компонентов, поступающих на вход модели,
- задание числа компонентов, обрабатываемых в системе
- и др.
Чтобы результаты, полученные на имитационной модели, были статистическими значимы, стремятся повысить точность результатов моделирования, повторяя эксперимент и усредняя полученные результаты. Этот способ неэффективен, т.к.:
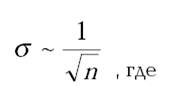
n – число повторений.
Вопрос: как много выборочных значений следует взять, чтобы обеспечить статистическую значимость результатов моделирования.
Задача состоит в том, чтобы определить при заданной точности необходимое число прогонов. Задача является обратной рассмотренной выше задачи оценивания точности методом доверительных интервалов.
Задача состоит в определении необходимого для выполнения (6.5) объема выборки n.
В предположении нормальности распределения выборочных значений из генеральной совокупности можно показать, что n = (  2/ d2, где
2/ d2, где  -двусторонняя станд.нормальная статистика.
-двусторонняя станд.нормальная статистика.
Для решения n необходимо знать  ,
,  , d.
, d.
На практике проводят пробные прогоны и поступают следующим образом:

n – необходимое число прогонов;
n0 – количество пробных прогонов;
d0 – доверительный интервал, оцененный по результатам пробного прогона;
d – требуемая точность.
Анализ установившегося состояния. Определение участка разгона (разогрева) модели для исключения неустановившихся режимов функционирования системы.
Установившимся (стационарным) называется такое состояние модели, когда последовательные наблюдения отклика в установившемся состоянии имеют некоторое предельное стационарное распределения вероятностей, не зависят от времени.
Стационарность режима моделирования характеризует собой некоторое установившееся равновесие процессов в модели системы Часто говорят, что динамическая система находится в равновесии (стационарном состоянии), если её функционирование происходит в соответствии с параметрами предельного стационарного распределения, которое не зависит от времени (т.е. если имитировать и дальше, то новой информации не получишь и продолжение имитации будет являться бессмысленной тратой времени). Обычно имитационные модели применяются для изучения системы в типичных условиях. Установившееся состояние обычно характерно для типичных условий функционирования (для систем массового обслуживания не естественны начальные состояния (0,0) – “пуст и свободен”), например, процессы обслуживания в аэропорту, на транспорте, в больнице.
В некоторых стохастических моделях требуется некоторое время для достижения моделью необходимого установившегося состояния, имитационная модель не сразу выходит в стационарный режим работы. Необходимо определить момент достижения стационарного режима моделирования и позаботиться об уменьшении влияния начального периода моделирования или его исключения из результатов моделирования. Очевидно, что если исследовать только установившийся режим, то качество статистических оценок повысится. Чтобы исключить влияние начального периода на результаты моделирования можно предложить:
• Использование длинных прогонов модели (если позволяет машинное время) для достижения статистического равновесия. Недостаток такого подхода – требуется много машинного времени.
• Исключение из рассмотрения начального периода прогона. Продумывают процедуры отсечения, когда имитационная модель выходит в установившийся режим, в этот момент уничтожают предыдущую статистику. Недостаток – надо контролировать результаты моделирования, при этом сложно определить установившееся состояние в условиях стохастической модели, кроме того машинное время тратится не на имитацию, а на анализ установившегося режима.
• Выбор такого начального условия, которое ближе всего к типичному, тем самым достигается существенное уменьшение длительность переходного режима в модели. Для этого проводят пробный прогон, чтобы определить момент выхода системы в стационарный режим.
Однако рассмотренной процедурой надо пользоваться аккуратно, т.к. для некоторых исследуемых процессов переходный режим может представлять самостоятельный интерес.
Обсуждение других задач тактического планирования можно найти в специальной литературе [20,33].
Дата добавления: 2014-12-15; просмотров: 278 | Поможем написать вашу работу | Нарушение авторских прав |