Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Математическая постановка задачи

В настоящей работе рассматривается движение симметричного бинарного раствора электролита между полупроницаемыми мембранами. Коэффициент диффузии катионов и анионов полагается равным D, динамическая вязкость – μ и диэлектрическая проницаемость среды – ε. Поверхности мембран заданы уравнениями y = 0 и y = L. Тильдой помечаются безразмерные величины, в отличие от их размерных аналогов. {x, y} есть координаты системы, где x и y – направления вдоль поверхности мембран и нормаль к ней, соответственно.

Ниже перечислены характерные величины, при которых система принимает безразмерный вид:
— характерная длина, расстояние между мембранами;
— характерное время;
— динамическая вязкость;
— термодинамический потенциал;
— нейтральная концентрация ионов в начальный момент времени.

Здесь — постоянная Фарадея, — универсальная газовая постоянная, — абсолютная температура в Кельвинах. В безразмерных переменных течение заключено между стенками y = 0 и y = 1.

Возникновение электроконвекции описывается уравнениями переноса ионов, уравнением Пуассона для электрического потенциала и уравнениями Стокса для вязкой жидкости

(1)
, (2)

(3)

и — концентрации катионов и анионов. Вначале был рассмотрен двумерный случай, где — вектор скорости, — электрический потенциал, — давление, — безразмерное число Дебая, которое есть ни что иное, как отношение к ,

и — коэффициент сцепления между гидродинамической и электростатической частями системы,

.

Данный параметр характеризует физические свойства раствора электролита и является его постоянным значением.

В случае двумерного течения, вместо уравнения (3) может быть рассмотрено следующее уравнение для функции тока, :

. (4)
На поверхностях мембран выполняются следующие краевые условия:

(5)
(6)
Первое краевое условие, описывающее концентрацию ионов на поверхности раздела мембраны и электролита, имеет место для достаточно больших и было впервые введено Рубинштейном (см, например, [13] и соответствующие ссылки). Второе условие означает равенство нулю потока анионов, третье — разность потенциалов фиксирована и последнее — выполняются условие прилипания. Предполагается, что пространственная область бесконечна в направлении оси абсцисс, и в качестве дополнительного условия рассматриваются только решения, ограниченные при .

Добавление начальных условий для концентрации ионов замыкает систему (1) – (6). Эти условия возникают из следующих соображений: когда разность потенциалов между мембранами отсутствует, распределение ионов является однородным и нейтральным. Это соответствует начальному условию . На это распределение ионов должны быть наложены некоторые типы возмущений:

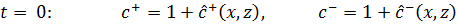(7)
Были рассмотрены два типа начальных условий вида (7):

(a) Начальные условия для концентраций ионов, естественные с точки зрения эксперимента. Так называемые “комнатные возмущения'', определяющие внешний малоамплитудный шум:

(8)

(b) Искусственные монохроматические возмущения с фиксированным волновым числом ,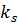

. (9)

На поверхности мембраны в процессе расчета вычислялась плотность тока , связанная с предельным значением ,

(10)
Для дальнейшего анализа удобно ввести средние величины электрического тока по длине и по времени

(11)

Задача описывается тремя безразмерными параметрами: разностью потенциалов – , малым параметром – ν и коэффициентом ϰ. Зависимость от для сверхпредельных режимов весьма слабая, поэтому разумно не включать ее в число параметров.

Задача решалась для безразмерная разность потенциалов менялась в пределах . Во всех расчетах принималось . (Некоторые расчеты были выполнены при значениях и . Для сверхпредельных режимов результаты всех этих расчетов согласуются с результатами вычислений для .)

Типичными являются следующие значения величин: основная масса концентрации водного раствора электролита изменяется в пределах моль/ ; разность потенциалов V; абсолютная температура К; коэффициент диффузии , расстояние между электродами – величина порядка ; значение на поверхности мембраны должно быть намного больше, чем и во всех расчетах обычно принималось равным от до . Безразмерная толщина слоя , зависящая от концентрации , варьируется в диапазоне от 1 до 100 нм.