Читайте также:
|
A. Дискретизация системы Нернста-Планка-Пуассона-Стокса
Для получения дискретного описания системы (1) – (3) была использована конечно-разностная аппроксимация второго порядка точности по пространству. В соответствии с неравномерностью узлов расчетной сетки все скалярные величины (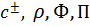
) определены в центре ячеек, в то время как компоненты скорости отыскиваются в центрах граней каждой ячейки. По нормали к твердым стенкам строится неравномерная сетка со сгущением узлов в пристенной области с помощью функции th, что позволяет удобно аппроксимировать граничные слои вблизи мембранных поверхностей. В направлении оси Ox поле является однородным, поэтому и сетка в этом направлении равномерна. Дискретизация линейных членов системы (1) – (3), так же как и постановка граничных условий не представляет больших трудностей. Для более подробного ознакомления отсылаем читателя к работе [37] и др. Нелинейные члены в (1), записанные в дивергентной форме
u ·∇ 
∓ ∇·( ∇ 
) ≡ ∇·( (u ∓ ∇ )), заменены центральными разностями с использованием интерполяции второго порядка функции , которая необходима для того, чтобы определить значение данной функции в центре грани ячейки по известным значениям в центрах самих ячеек.
В результате данной дискретизации задача сводится к решению системы обыкновенных дифференциальных уравнений (ОДУ)
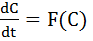. (12)
Здесь 
– вектор размерности 
, состоящий из 
значений сеточной функции 
и значений функции 
. 
— общее количество ячеек расчетной сетки, где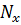 
и 
– количество узловых точек по соответствующим направлениям в пространстве. Вектор – функция 
включает в себя как нелинейные, так и линейные члены, полученные с помощью дискретизации уравнения (1).
Дата добавления: 2014-12-15; просмотров: 139 | Поможем написать вашу работу | Нарушение авторских прав |