
Читайте также:
|
В евклидовых пространствах вводится понятие скалярного произведения, а уже на его основе определяется норма.
Пусть в действительном линейном пространстве L задан функционал L× L →R. Значение этого функционала называется скалярным произведением и обозначается  ,
,  L y
L y 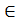 L, если выполняются следующие условия:
L, если выполняются следующие условия:
1.  L: x, x
L: x, x  0.
0.
2. x, x  0
0 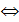 x
x  0.
0.
3. λ x,y =λ x, y, λ  R.
R.
4. x1 +x2, y =x1, y + x2, y.
5. x, y =y, x.
Линейное пространство с заданным в нем скалярным произведением называется евклидовым пространством. Иногда евклидовы пространства называются предгильбертовыми пространствами, а для скалярного произведения используется обозначение x / y. Норма в евклидовом пространстве вводится формулой
 =
=  .
.
Можно проверить, что все аксиомы нормы оказываются при этом выполненными. В евклидовом пространстве может быть задан угол между векторами. Для ненулевых векторов, x 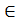 L y
L y 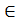 L угол определяется выражением
L угол определяется выражением

Можно доказать, что, как и должно быть, правая часть равенства не превосходит единицы. Если для ненулевых векторов x 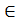 L, y
L, y 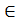 L имеем, x, y = 0, то
L имеем, x, y = 0, то  = π/2, а векторы x и y называются ортогональными. Система ненулевых векторов
= π/2, а векторы x и y называются ортогональными. Система ненулевых векторов  из L называется ортогональной, если они попарно ортогональны:
из L называется ортогональной, если они попарно ортогональны:
α 
 = 0.
= 0.
Счетность множества x не предполагается.
Дата добавления: 2015-02-16; просмотров: 110 | Поможем написать вашу работу | Нарушение авторских прав |
|