Читайте также:
|
Статическая устойчивость сложных электроэнергетических систем
Уравнения малых колебаний ЭЭС
Исходная система нелинейных дифференциальных уравнений, описывающая динамику поведения ЭЭС при возмущениях, в общем виде может быть представлена как
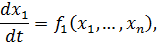
(4.1)
 | |
|
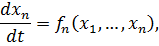
где переменные xi,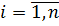 
, представляют, например, углы и скольжения роторов генераторов при описании динамики ЭЭС уравнениями движения генераторов и представлении каждого уравнения движения второго порядка двумя дифференциальными уравнениями первого порядка.
Поскольку рассматриваются малые колебания роторов генераторов под воздействием малых возмущений, исходные нелинейные дифференциальные уравнения (4.1) могут быть линеаризованы путем разложения правых частей (4.1) в ряд Тейлора и рассмотрения лишь первых членов ряда Тейлора. Тогда в отклонениях переменных система (4.1) превращается в следующую систему линейных дифференциальных уравнений
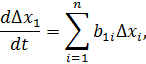
(4.2)
где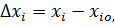 
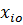- значение переменной в установившемся режиме, в котором исследуется статическая устойчивость ЭЭС.
В матричной форме записи система уравнений (4.2) выглядит как
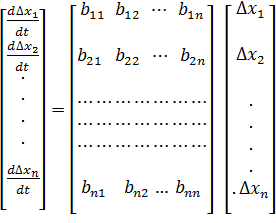(4.3)
или в компактном виде
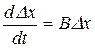(4.4)
Дата добавления: 2015-02-16; просмотров: 86 | Поможем написать вашу работу | Нарушение авторских прав |