Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Критерий Рауса-Гурвица

Англичанин Раус в 1873 г. предложил, а швейцарец Гурвиц в 1885 г. формализовал алгебраический критерий устойчивости. В настоящее время он известен как критерий Рауса-Гурвица, который формулируется следующим образом.

Для устойчивости системы требуется, чтобы коэффициенты характеристического уравнения были положительными, а также удовлетворяли некоторым соотношениям. Критерий Рауса-Гурвица устанавливает эти соотношения в форме неравенств, соблюдение которых является необходимым и достаточным условием устойчивости системы любого порядка.

Система неравенств Гурвица строится следующим образом. Из коэффициентов характеристического уравнения n -й степени (4.6) составляется квадратная матрица n -го порядка

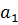
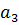
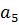
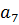…….. 0 0 0

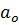
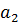
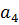
…… 0 0 0

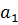
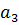
0 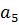……… 0 0 0

…………………………………………………. (4.17)

0 0 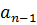0 …… 0

0 0 0 ……

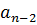
Правило оставления матрицы Гурвица следующее. По главной диагонали располагают коэффициенты характеристического многочлена (4.7) в порядке их нумерации с 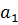до 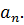В строках помещаются поочередно коэффициенты только с нечеткими или только с четкими индексами (включая коэффициент 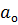), причем влево от диагонали с уменьшающимися, вправо с увеличивающимися индексами. Все недостающие коэффициенты, т.е. коэффициенты с индексами меньше нуля или больше n, заменяются нулями.

Для обеспечения устойчивости требуется, чтобы все n диагональных миноров матрицы (4.17) были положительными. Диагональные миноры (называемые определителями Гурвица) получаются отчеркиванием их справа и снизу, как показано в (4.17). Таким образом, критерий Рауса-Гурвица записывается как

(4.18)

Заметим, что последний определитель 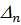включает в себя уже всю матрицу Гурвица целиком. Если его раскрыть по элементам последнего столбца, содержащего только коэффициент , то можно записать

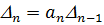. (4.19)

Гурвиц показал, что если непрерывно изменять коэффициенты характеристического уравнения, ухудшая устойчивость системы, то при потере устойчивости в нуль прежде всего обратится определитель 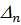, если при этом 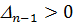, то, следовательно, граница устойчивости определяется условием =0. Это граница апериодической устойчивости (один действительный корень находится на мнимой оси плоскости корней). Если 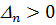, то в нуль обращается 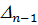, что соответствует наличию на границе пары чисто мнимых корней 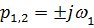. Это граница колебательной устойчивости. При переходе через эту границу начинается самораскачивание системы с частотой w ₁. Если и дальше продолжать изменять коэффициенты характеристического уравнения, то могут стать отрицательными и другие определители Гурвица, а 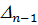вновь может стать положительным. Поэтому положительность и 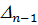(а значит, и 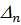) еще не свидетельствует об устойчивости, должны быть положительными и другие определители Гурвица.