Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Устойчивость в малом по А.М. Ляпунову

Исторически первое систематическое исследование свойств устойчивости уравнения (системы уравнений (4.1) при надлежит А.М. Ляпунову, который рассмотрел следующую задачу: если начало координат является точкой (положением) равновесия системы (4.1), т.е. f (0)=0 для всех t, и если система выведена из равновесия, останутся ли траектории процесса «близкими» к началу координат для всех последующих моментов времени. В геометрической форме эта ситуация представлена на рис. 4.1. Основная идея состоит в том, что, если процесс начинается в пределах небольших расстояний от начала координат, он должен оставаться внутри некоторого «канала», показанного на рис. 4.1 штриховой линией.

Несколько более сильное определение устойчивости отвечает требованию при , т.е. чтобы система в конечном счете возвращалась в положение равновесия. Такое определение соответствует понятию асимптотической устойчивости (согласно А.М. Ляпунову), в отличие от просто устойчивости, трактуемой так, как это сделано выше со ссылкой на рис. 4.1.

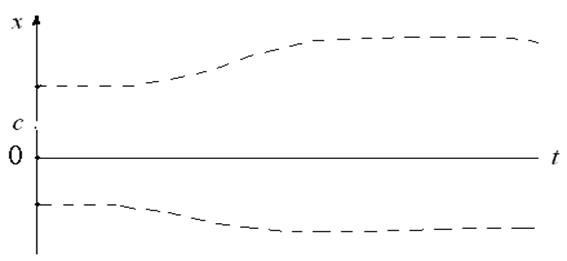
Рис. 4.1. Устойчивость по Ляпунову

Заметим, кстати, что приведенные выше стандартные определения устойчивости подразумевают, что заранее известно положение равновесия, в котором . Для сложных нелинейных систем, таких, как ЭЭС, положений равновесия достаточно много. Для ЭЭС это доаварийные (или послеаварийные) установившиеся режимы. Их определение составляет непростую самостоятельную проблему.

Теорема об устойчивости по первому приближению (статическая устойчивость в терминологии для ЭЭС), сформулированная А.М. Ляпуновым, дает следующие качественные характеристики устойчивости (рис. 4.2):

1) состояние равновесия асимптотически устойчиво, если все корни характеристического уравнения имеют отрицательные действительные части. Это положение верно и в случае, если корни кратные;

2) если у хотя бы одного корня характеристического уравнения положительная действительная часть, то положение равновесия неустойчиво;

3) если характеристическое уравнение имеет один простой корень с нулевой действительной частью (т.е. два чисто мнимых сопряженных корня или один нулевой корень), то положение равновесия устойчиво, но асимптотической устойчивости нет;

4) если у характеристического уравнения два нулевых корня, то положение равновесия неустойчиво.

На рис. 4.2 p ₁ и p ₂, p ₄ и p ₅, p ₈ и p ₉ – пары комплексно сопряженных корней.

Решение для системы (4.4) можно записать в виде:

Рис. 4.2. Расположение корней на комплексной

плоскости

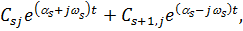(4.10)

где и всегда (при любых начальных условиях) комплексно сопряженные

(4.11)

Поэтому (4.10) после некоторых преобразований можно записать в виде

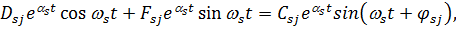(4.12)

где

Рис. 4.3. Характер процесса во времени при разном расположении корней

На рис. 4.3 показаны особенности переходных процессов при различном расположении корней характеристического уравнения на комплексной плоскости корней, показанных на рис. 4.2: 1 – р ₃; 2 – р ₇; 3 – р ₁, р ₂; 4 – р ₈, р ₉. Случаи 1 и 2 соответствуют апериодически устойчивой и неустойчивой системе, а случаи 3 и 4 – колебательно устойчивой и неустойчивой, соответственно.