Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Критерий А.В. Михайлова

А.В. Михайлов в 1938 г. предложил для оценки статической устойчивости принцип аргумента, известный из теории функций комплексного переменного. Поясним этот принцип.

Пусть имеем многочлен в виде (4.13), приравненный к нулю (характеристическое уравнение). Корень можно представить на плоскости корней вектором с модулем и соответствующим углом между и осью абсцисс, при этом отсчет углов выполняется против часовой стрелки (см. рис. 4.4, а).

р

a a

Рис. 4.4. Положения векторов, представляющих корни характеристического уравнения

Положим , т.е. направим вектор р по мнимой оси. Тогда конец вектора лежит на мнимой оси. При изменении w он скользит по мнимой оси (рис. 4.4, б).

При изменении w от -¥ до +¥ аргумент вектора получает приращение, равное p, если , и приращение, равное -p, если

Характеристический многочлен 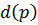при представляет собой характеристический вектор

, (4.20)

модуль и аргумент которого определяются как

, (4.21)

(4.22)

Если среди n корней характеристического уравнения корней лежат в правой полуплоскости, а корней – в левой, то приращение 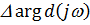при изменении w от -¥ до +¥ будет равно

. (4.23)

Выражение (4.23) называется правилом аргумента.

Для устойчивой системы и из (4.23) имеем

. (4.24)

Критерий А.В. Михайлова является геометрической интерпретацией правила аргумента, выполняемой следующим образом.

Вектор можно представить как

. (4.25)

При изменении w от -¥ до +¥ вектор вращается против часовой стрелки и своим концом описывает кривую, называемую характеристической кривой или годографом характеристического уравнения. На рис. 4.5, а показана часть годографа при изменении w от 0 до +¥.

Представим составляющие характеристического вектора в развернутом виде:

(4.26)

(4.27)

Поскольку в 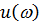входят только четные степени w, то

(4.28)

Поскольку в входят только нечетные степени w, то

(4.29)

С учетом (4.28) видим, что годограф симметричен относительно действительной оси (см. рис. 4.5, б), т.е. годограф устойчивой системы при изменении w от 0 до +¥ повернется на угол или на n квадрантов.

			u

		w ®+¥
		w ®-¥
	Рис. 4.5. Годограф характеристического уравнения

На рис. 4.6 в качестве примера показан вид годографа устойчивой системы при n =5 и зависимости составляющих характеристического вектора от w. На рис. 4.7, 4.8 представлены аналогичные кривые для неустойчивых систем при n =5.

		a
		w
		a

Рис. 4.6. Вид годографа устойчивой системы при и зависимости составляющих характеристического вектора от

v u, v

Рис. 4.7. Вид годографа неустойчивой системы при n =5, случай 1 (а), и зависимости составляющих характеристического вектора от

Рис. 4.8. Вид годографа неустойчивой системы при n =5, случай 2 (а), и зависимости составляющих характеристического вектора от