Читайте также:
|
Одна из задач, где необходимо знание корней характеристического уравнения – построение внутри областей устойчивости границ равных значений степени устойчивости.
Степень устойчивости системы определяется как
, (4.35)
т.е. это наименьшее из абсолютных значений действительных частей все корней характеристического уравнения или расстояние от мнимой оси до ближайшего корня устойчивой системы.
Величина степени устойчивости может служить приближенной оценкой быстроты затухания переходного процесса (см. структуру решения системы линейных дифференциальных уравнений в (4.12)).
Пусть имеем характеристическое уравнение в виде (4.6), (4.7). На плоскости корней 
сместим мнимую ось влево на расстояние l (рис. 4.10, а). Получим новую плоскость 
(см. рис. 4.10, б).
Преобразуем исходное характеристическое уравнение к новой переменной g. Для этого в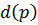 
заменим 
на 
и получим 
Разложим 
в ряд по степеням g -
 | |||
 | |||
Рис. 4.10. Смещение мнимой оси на плоскости корней.
(4.36)
где штрихами обозначены производные по g от 
. Ограничимся членами ряда со степенью 
, где n – порядок характеристического уравнения.
Поскольку 
, получим смещенное характеристическое уравнение в виде
(4.37)
где 
т.е. коэффициенты смещенного характеристического уравнения выражаются через коэффициенты исходного характеристического уравнения и зависят от величины смещения l мнимой оси.
При смещении, равном степени устойчивости, когда одна пара комплексных или один действительный корень будут лежать на смещенной мнимой оси w ’, смещенное характеристическое уравнение будет соответствовать системе, находящейся на границе области устойчивости.
С помощью метода D-разбиения можно построить область для смещенного характеристического уравнения. Она меньше, чем область устойчивости при l =0. При увеличении l область уменьшается. При значении l, равном степени устойчивости, область превращается в точку.
В качестве примера использования изложенного подхода рассмотрим задачу выбора оптимальных значений коэффициентов регулирования АРВ, например, по отклонению частоты и ее производной в АРВ СД. Конфигурация области устойчивости в плоскости этих коэффициентов имеет вид кривой 1 на рис. 4.11.
На рис. 4.11 для кривой 1 
. Далее 
; 
; 
; 
.
Точка 5 соответствует оптимальным значениям коэффициентов регулирования АРВ, которые обеспечивают максимальное демпфирование колебаний.
 |
Рис. 4.11. Иллюстрация оптимального выбора коэффициентов регулирования АРВ
Дата добавления: 2015-02-16; просмотров: 73 | Поможем написать вашу работу | Нарушение авторских прав |