Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Плотность множества действительных чисел.

Теорема 1. Множество D плотно в множестве действительных чисел, т.е. между любыми двумя не равными действительными числами находится конечная десятичная дробь.

Доказательство:

2.

3.

1. такое n по определению отношения “<”. Покажем, что дважды равенство получится не может ОП: 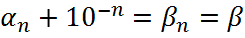, начиная с какого-то n, тогда:

= 9, начиная с некоторого индекса, а это невозможно по определению R числа?! Таким образом, (1) одно из нестрогих неравенств является строгим для некоторого индекса n, тогда равенство

2. Между и находится 0, а это конечная десятичная дробь.

3. ó Согласно первому случаю такая конечная десятичная дробь , что , а следовательно . ч.т.д.

Следствие: Пусть последовательность, где каждое десятичная дробь с n знаками после запятой. И пусть такие, что:

Доказательство: Пусть .

по предыдущей теореме из того, что => конечные десятичные дроби s и t, что , тогда - = , .!? (противоречит архимедовости).