Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Порядок в поле рациональных чисел

Умножение и деление натуральных чисел

Определение: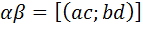

Теорема 1: определение произведения рациональных чисел корректно.

Док-во: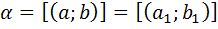

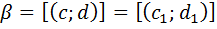
Нужно доказать:

·

·

.

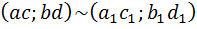
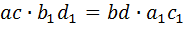
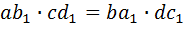Теорема 2: умножение рациональных чисел коммутативно, ассоциативно, дистрибутивно относительно сложения.

Док-во: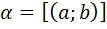

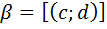
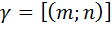
1) ?

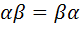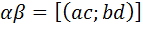
умножение целых чисел коммутативно

2)

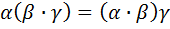
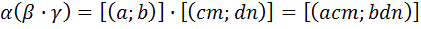
3)

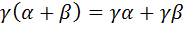
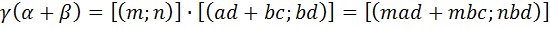
4) .

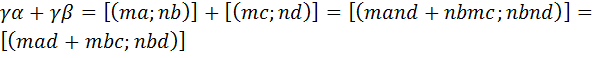Утверждение 1: рациональное число: является нейтральным элементом относительно умножения в мн-ве Q.

Утверждение 2: для любого рационального числа: обратным является число:

Следствие: поле

Порядок в поле рациональных чисел

Утверждение 1. Произвольное рациональное число является классом пары, где а ÎN, в Î Z.

Доказательство: (а, в)~(а(-1), в(-1))=(-а, -в). Ä

Поэтому дальше будем использовать пары только с положительным вторым элементом.

Определение 1: Пусть a=[(а, в)], b=[(с, d)] ÎQ. Будем говорить a>b если ad>bc.

Теорема 1: Определение 1 корректно.

Теорема 2: " a,bÎ Q могут находиться только в одном соотношении: a>b Ú a=b Ú a<b.

Теорема 3: Отношение «≥» является отношением порядка на Q.