Читайте также:
|
Пусть 
множество сигналов, объединенных как объекты с некоторыми общими свойствами, характерными для множества М.
Исследование сигналов, образующих такие множества очень плодотворно, так как позволяет представлять, или определять одни сигналы множества М через другие сигналы того же множества.
Принято говорить, что множество сигналов М наделено определенной структурой, которая выбирается из физических соображений. Так, применительно к электрическим колебаниям известно, что они могут умножаться на произвольный масштабный коэффициент. Это дает возможность в множествах сигналов ввести структуру линейного пространства.
Множество сигналов М образует вещественное линей2ное пространство, если справедливы следующие аксиомы:
1. Любой линейный сигнал 
при любых t принимает лишь вещественные значения.
2. Для любых и 
существует их сумма 
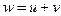, причем w также содержится в М, т.е. 
. Операция суммирования коммутативна 
и ассоциативна 
.
3. Для любого сигнала 
и любого вещественного числа α определен сигнал 
.
4. Множество М содержит особый нулевой элемент 0, такой, что u+0=u для всех 
,
Если математические модели сигналов приводят к получению комплексных значений сигналов, то, допуская в аксиоме 3 умножение на комплексное число, приходим к понятию комплексного линейного пространства.
Введение структуры линейного пространства является первым шагом на пути к геометрической трактовке сигналов. Элементы линейных пространств сигналов часто называют векторами. Отметим, что ограничения, накладываемые аксиоматикой линейных пространств, очень жесткие и не каждое множество сигналов оказывается линейным пространством.
Дата добавления: 2015-04-11; просмотров: 96 | Поможем написать вашу работу | Нарушение авторских прав |