Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Вывод кривой Филипса

Для вывода стандартной неокейнсианской кривой Филипса, используют оптимальное правило ценообразования (28):

(28)

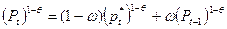Кроме того, из определения (7) и предположения Кальво, заметим, что индекс цен можно записать как средневзвешенное новых цен и индекса цен предыдущего периода [39]:

(39)

Далее, определим как относительную цену, которую выбирают фирмы, пересматривающие свои цены в периоде t, и заметим, что в устойчивом состоянии и .[40]

Деление (39) на дает:

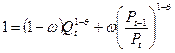(40)

Разделив (40) на и линеаризируя (точно также, как ранее) около устойчивого состояния, получаем:

(41)

что эквивалентно

(42)

Вспомним, что из (29) и . Используя предыдущие два уравнения, оптимальное правило фирм для установления цен (28) можно переписать следующим образом:

(43)

Перепишем сначала левую часть уравнения (43) в следующем виде:

(44)

где натуральные логарифмы соответствующих величин .

Применим аппроксимацию Тейлора около , принимая во внимание, что в устойчивом состоянии и , так как . Чтобы не путаться, напишем подробнее и .

(45)

Далее, сумма ряда 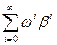, очевидно, равна , так как . Группируя члены, получаем:

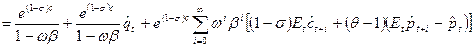[41] (46)

Аналогично, записывая правую часть уравнения (43) в измененном виде и используя аппроксимацию Тейлора около , получаем:

[42] (47)

и

(48)

Снова аппроксимируя бесконечную сумму и группируя, получим:

[43] (49)

Приравнивая (46) и (49) получаем:

(50)

заметим, что . Получаем:

(51)

Сокращение одинаковых членов в левой и правой частях уравнения приводит к уравнению:

(52)

или, вынося из суммы:

(53)

Умножение обеих частей уравнения на и прибавление к ним дает:

(54)

В соответствии с полученным выражением, процентное отклонение номинальной оптимальной цены [44] равно (примерно) ожидаемому дисконтированному объему будущих процентных отклонений номинальных предельных издержек (или просто правой части уравнения). Это выражение можно записать в рамках двухпериодной модели, в которой отсутствуют члены выше второй степени, а заменено на 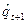согласно (29)[45]:

(55)

Преобразовывая, получаем:

(56)

Используя (42), имеем:

(57)

Затем, умножая обе части на величину , получаем стандартный вид неокейнсианской кривой Филипса, в котором инфляция представляет собой функцию от процентного отклонения реальных предельных издержек и ожидаемой инфляции

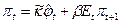
с

На данный момент мы нашли формулу для инфляции, которая зависит от реальных предельных издержек. Вывод кривой Филипса, которая зависела бы от разрыва выпуска (output gap), можно провести следующим образом. Во-первых, как было показано в (20) реальная заработная плата равна предельной норме замещения между отдыхом и потреблением:

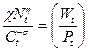(20)

или в терминах процентных отклонений около устойчивого состояния, используя :

Во-вторых, заметим, что согласно (24) реальные предельные издержки фирмы равняются реальной заработной плате разделенной на предельный продукт труда . Следовательно, выражая (24) в терминах процентных отклонений вокруг устойчивого состояния, получаем:

В-третьих, заметим, что, если , то в (32) можно представить:

Тогда, можно записать:

(60)

Так как равновесный выпуск в условиях гибких цен задается согласно (34) как:

То (60) можно переписать в виде:

(61)

и неокейнсианская кривая Филипса в (58) приобретает следующий вид:

(62)

где - разрыв выпуска (output gap), то есть разница между фактическим выпуском и выпуском при гибких ценах (точнее, процентных отклонений), и:

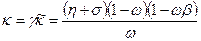(63)

В дополнение, опишем кривую Филипса, на которую дополнительно будет влиять инфляционный шок (inflation shock)[46]. Кларида, Гали и Гертлер (Clarida, Gali, Gertler, 2001) выступают за введение в модель такого рода шоков. Они добавляют стохастическую надбавку к заработной плате, чтобы показать отклонения между предельной нормой замещения между отдыхом и потреблением и реальной заработной платой. Тогда, (20) можно записать следующим образом:

(64)

Где - случайное искажение. Оно может возникнуть из-за изменений предпочтений, которые влияют на предельную полезность досуга. Или, в случае несовершенной конкуренции на рынке труда, оно может возникнуть из-за случайных сдвигов надбавки заработной платы относительно предельной нормой замещения (Clarida, Gali, Gertler 2002).

Линеаризация уравнения (64) дает:

(65)

и, выполнив преобразования, аналогичные проделанным в (60), получим выражение для реальных предельных издержек

(66)

Тогда неокейнсианская кривая Филипса:

(67)

где – инфляционный шок. Заметим, что добавление шока предложения в наш анализ также влияет на равновесный выпуск при гибких ценах.