
Читайте также:
|
Для функции одной переменной имеем

Рассмотрим функцию f(x, y). Положим x = a + t Δx, y = b + t Δy. Здесь a, b, Δxи Δy – фиксированные значения, t – переменная величина. Тогда функция f (a + t Δx, b + t Δy) становится функцией только одной переменной t. Формула Тейлора для нее принимает вид (n = 2)

Дифференциал второго порядка.
 - полный дифференциал первого порядка.
- полный дифференциал первого порядка.
d(dz) =d2z – дифференциал второго порядка.
d2z =  - дифференциал второго порядка от функции двух переменных z = f (x, y)/
- дифференциал второго порядка от функции двух переменных z = f (x, y)/
Повторное дифференцирование.
Рассмотрим функцию z = f(x, y). Найдем 
От этих производных можно также найти производные

Аналогично находятся производные более высоких порядков.
Например, z = x3 – 4x2y + 5y2,



 Теорема.
Теорема.  Если функция z = f(x, y) и ее частные
Если функция z = f(x, y) и ее частные
производные f′x, f′y, f′′xy, f′′yx непрерывны в точке (х, у)
 то
то 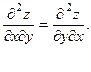
 Из этой теоремы вытекает, что
Из этой теоремы вытекает, что




Дата добавления: 2015-09-10; просмотров: 82 | Поможем написать вашу работу | Нарушение авторских прав |