Читайте также:
|
Дано: 
, 
, 
.
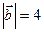Решение.
По условию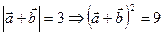 
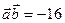
Получим: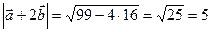 
Ответ: 
Билет №18.
Задача №1. Постойте отрезок 
, где а и с – длины данных отрезков.
Дано: отрезки a и c
Построить: 
Построение.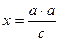 
1) На одной стороне произвольного угла от его начала откладываем отрезки c и a;
2) На второй стороне угла откладываем отрезок а;
3) Проводим прямую через концы отрезков с и а и параллельно ей проводим прямую через конец отрезка а;
4) Получившийся отрезок х – искомый (по теореме Фалеса).
Задача №2. По данным четырём отрезкам a, b, c, d постройте трапецию с основаниями a и b. При каком соотношении между длинами этих отрезков это невозможно?
Дано: отрезки a, b, c, d
Построить: трапецию, где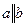 
Построение.
1) Построим 
со сторонами c, d, a-b
2) Достроим получившийся треугольник до параллелограмма
3) оставшаяся часть – искомая трапеция.
Билет №19.
Задача №1. Найдите острые углы треугольника АВС, если <АВС=900, АС=2 
, ВК=1, где СК – высота треугольника.
Дано: 
- прямоугольный, 
,
, 
, СК – высота
Решение.
Пусть 
, тогда по теореме о высоте, опущенной из вершины прямого угла 
- не удовлетворяет условию задачи
: 
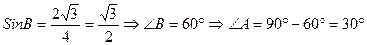
Ответ: 
, 
.
Задача №2. В треугольник АВС вписана окружность. С1, В1 – точки её касания со сторонами АВ и АС соответственно; АС1=7, ВС1=6, В1С=8. найдите радиусы вписанной и описанной около треугольника АВС окружностей.
Дано: , 
, 
, 
, 
и 
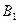- точки касания Окр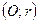 
Решение.
, 
, 
, как отрезки касательных, выходящих из одной точки.
Тогда 
, 
, 
, 
По формуле Герона: 
, с другой стороны 
Ответ: 
, 
Билет №20.
Дата добавления: 2015-09-10; просмотров: 127 | Поможем написать вашу работу | Нарушение авторских прав |