
Читайте также:
|
Мы повторим здесь определение непрерывности функции, данное выше, в главе о пределах.
Определение 3.1 Пусть функция  определена на некотором интервале
определена на некотором интервале  , для которого
, для которого  -- внутренняя точка. Функция
-- внутренняя точка. Функция  называется непрерывной в точке
называется непрерывной в точке  , если существует предел
, если существует предел  при
при  и этот предел равен значению
и этот предел равен значению  , то есть
, то есть

Пусть функция  определена на некотором полуинтервале
определена на некотором полуинтервале  , для которого
, для которого  -- левый конец. Функция
-- левый конец. Функция  называется непрерывной справа в точке
называется непрерывной справа в точке  , если существует предел
, если существует предел  при
при  и этот предел равен значению
и этот предел равен значению  , то есть
, то есть

Пусть, наконец, функция  определена на некотором полуинтервале
определена на некотором полуинтервале  , для которого
, для которого  -- правый конец. Функция
-- правый конец. Функция  называется непрерывной слева в точке
называется непрерывной слева в точке  , если существует предел
, если существует предел  при
при  и этот предел равен значению
и этот предел равен значению  , то есть
, то есть

Из теоремы о связи двустороннего предела с односторонними (теорема 2.1) сразу следует, как уже отмечалось в главе 2, что имеет место следующее предложение.
Предложение 3.1 Функция  тогда и только тогда непрерывна в точке
тогда и только тогда непрерывна в точке  , когда она непрерывна в точке
, когда она непрерывна в точке  справа и слева, то есть когда выполнены следующие условия:
справа и слева, то есть когда выполнены следующие условия:
1) функция  определена в точке
определена в точке  и в некоторой окрестности этой точки;
и в некоторой окрестности этой точки;
2) существует предел значений функции слева:  ;
;
3) существует предел значений функции справа:  ;
;
4) эти два предела совпадают между собой и со значением функции в точке  :
:  .
.

Рис.3.1.Функция непрерывна: пределы слева и справа совпадают с 
Точка  , в которой функция непрерывна, называется точкой непрерывности функции
, в которой функция непрерывна, называется точкой непрерывности функции  ; так же определяются точки непрерывности слева и справа.
; так же определяются точки непрерывности слева и справа.
Пример 3.1 Пусть  и
и  . Тогда
. Тогда  и
и  . Эти значения совпадают, значит, функция
. Эти значения совпадают, значит, функция  непрерывна в точке
непрерывна в точке  .
.
(Функция  -- элементарная функция;
-- элементарная функция;  -- точка её области определения
-- точка её области определения  . Все элементарные функции непрерывны во всех внутренних точках своих областей определения, в том числе и эта. Так что в этом примере можно было бы заменить
. Все элементарные функции непрерывны во всех внутренних точках своих областей определения, в том числе и эта. Так что в этом примере можно было бы заменить  любой элементарной функцией, а
любой элементарной функцией, а  -- любой внутренней точкой области
-- любой внутренней точкой области  , и вывод остался бы тем же.)
, и вывод остался бы тем же.)
Пример 3.2 Рассмотрим функцию  и точку
и точку  . При
. При  функция задаётся формулой
функция задаётся формулой  , при этом имеем
, при этом имеем  (первый замечательный предел). Это значение совпадает с тем, которое задано при
(первый замечательный предел). Это значение совпадает с тем, которое задано при  :
:  . Итак,
. Итак, 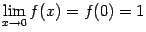 , что означает непрервыность функции
, что означает непрервыность функции  при
при  .
.
Тем, кто внимательно изучил данное в главе 2 общее понятие базы предела, можно предложить продумать и доказать следующее утверждение:
Предложение 3.2 Пусть  -- база непроколотых окрестностей точки
-- база непроколотых окрестностей точки  , окончаниями которой служат интервалы
, окончаниями которой служат интервалы  ,
,  ;
;  -- база непроколотых левых окрестностей точки
-- база непроколотых левых окрестностей точки  , окончаниями которой служат полуинтервалы
, окончаниями которой служат полуинтервалы 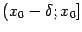 ,
,  ;
;  -- база непроколотых правых окрестностей точки
-- база непроколотых правых окрестностей точки  , окончаниями которой служат полуинтервалы
, окончаниями которой служат полуинтервалы  ,
,  . Тогда непрерывность функции
. Тогда непрерывность функции  в точке
в точке  эквивалентна тому, что существует предел
эквивалентна тому, что существует предел  ; непрерывность слева в точке
; непрерывность слева в точке  -- тому, что существует предел
-- тому, что существует предел  ; непрерывность справа в точке
; непрерывность справа в точке  -- тому, что существует предел
-- тому, что существует предел  .
.
СЛОЖНАЯ ФУНКЦИЯ
- функция, представленная как композиция нескольких функций. Если множество значений Yi функции fi содержится во множестве определения Х i+1 функции fi+1, т. е.

то функция  определяемая равенством
определяемая равенством

наз. сложной функцией или (п -1)-кратной композицией (суперпозицией) функций f1, f2,..., fn. Напр., всякая рациональная функция любого числа переменных является композицией четырех арифметич. действий, т. е. композицией функций х+у, x-у, ху, х/у.
С. ф. сохраняет многие свойства функций, композицией к-рых она является. Так, композиция непрерывных функций непрерывна. Это означает, что если функция  непрерывна в точке
непрерывна в точке  , а функция f2: Y
, а функция f2: Y  Z непрерывна в точке
Z непрерывна в точке 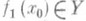 , то С. ф. f2 о/ f1 также непрерывна в точке х 0 (здесь X, Y и Zявляются, напр., топологии, пространствами). Подобным образом, композиция праз (непрерывно) дифференцируемых функций представляет собой также праз (непрерывно) дифференцируемую функцию, n=1, 2,... Композиция возрастающих (убывающих) функций есть возрастающая (соответственно убывающая) функция. При композиции функций иногда меняются количественные характеристики свойств функций: композиция функций f1 и f2, удовлетворяющих условию Гёльдера нек-рых степеней, есть функция, удовлетворяющая условию Гёльдера степени, равной произведению степеней условий Гёльдера, к-рым удовлетворяют функции f1 и f2. Нек-рые характеристики функций не сохраняются при композиции. Так, композиция функций, интегрируемых по Риману или по Лебегу, не является, вообще говоря, функцией, интегрируемой по Риману или, соответственно, по Лебегу; композиция абсолютно непрерывных функций может оказаться не абсолютно непрерывной функцией. Вместе с тем, согласно результатам Н. К. Бари и Д. Е. Меньшова [1], композиция трех абсолютно непрерывных на отрезке функций не приводит к новому классу функций по сравнению с композицией двух абсолютно непрерывных функций. Н. К. Бари [2] доказала, что любая непрерывная на отрезке функция может быть представлена в виде суммы трех композиций абсолютно непрерывных функций, и есть такие непрерывные функции, к-рые но могут быть представлены в виде суммы двух таких композиций. Вместе с тем, всякая непрерывная на отрезке функция является суммой двух композиций функций с ограниченным изменением; однако n-кратные композиции функций с ограниченным изменением для каждого п=1, 2,... приводят к существенно новым классам функций и существуют однократные композиции функций с ограниченным изменением, не являющиеся непрерывными функциями [3].
, то С. ф. f2 о/ f1 также непрерывна в точке х 0 (здесь X, Y и Zявляются, напр., топологии, пространствами). Подобным образом, композиция праз (непрерывно) дифференцируемых функций представляет собой также праз (непрерывно) дифференцируемую функцию, n=1, 2,... Композиция возрастающих (убывающих) функций есть возрастающая (соответственно убывающая) функция. При композиции функций иногда меняются количественные характеристики свойств функций: композиция функций f1 и f2, удовлетворяющих условию Гёльдера нек-рых степеней, есть функция, удовлетворяющая условию Гёльдера степени, равной произведению степеней условий Гёльдера, к-рым удовлетворяют функции f1 и f2. Нек-рые характеристики функций не сохраняются при композиции. Так, композиция функций, интегрируемых по Риману или по Лебегу, не является, вообще говоря, функцией, интегрируемой по Риману или, соответственно, по Лебегу; композиция абсолютно непрерывных функций может оказаться не абсолютно непрерывной функцией. Вместе с тем, согласно результатам Н. К. Бари и Д. Е. Меньшова [1], композиция трех абсолютно непрерывных на отрезке функций не приводит к новому классу функций по сравнению с композицией двух абсолютно непрерывных функций. Н. К. Бари [2] доказала, что любая непрерывная на отрезке функция может быть представлена в виде суммы трех композиций абсолютно непрерывных функций, и есть такие непрерывные функции, к-рые но могут быть представлены в виде суммы двух таких композиций. Вместе с тем, всякая непрерывная на отрезке функция является суммой двух композиций функций с ограниченным изменением; однако n-кратные композиции функций с ограниченным изменением для каждого п=1, 2,... приводят к существенно новым классам функций и существуют однократные композиции функций с ограниченным изменением, не являющиеся непрерывными функциями [3].
Понятие композиции функций представляет собой наиболее широкое понимание термина "представление функции формулой". Задача о представлении функций в виде композиций возникла в связи с отысканием формул для решений алгебраич. уравнений. Всякий кореньуравнения степени не выше четвертой может быть представлен формулой, выражающей его через коэффициенты уравнения и представляющей собой композицию четырех арифметич. действий и радикалов. Всякое уравнение степени  может быть с помощью подстановки (наз. преобразованием Чирнгаузена) приведено к виду
может быть с помощью подстановки (наз. преобразованием Чирнгаузена) приведено к виду

Таким образом, каждый корень уравнения степени  представляет собой функцию п- 4 параметров. Задача состоит в выяснении: можно ли эти функции представить в виде композиции алгебраич. функций меньшего числа неременных. Одна из 23 проблем Д. Гильберта (D. Hilbert), поставленных им на Международном конгрессе математиков в Париже в 1900, относилась к этой задаче. Именно, 13-я проблема состояла в следующем (см. [4]): представляется ли корень f уравнения
представляет собой функцию п- 4 параметров. Задача состоит в выяснении: можно ли эти функции представить в виде композиции алгебраич. функций меньшего числа неременных. Одна из 23 проблем Д. Гильберта (D. Hilbert), поставленных им на Международном конгрессе математиков в Париже в 1900, относилась к этой задаче. Именно, 13-я проблема состояла в следующем (см. [4]): представляется ли корень f уравнения
 (*)
(*)
через коэффициенты х, у и z этого уравнения посредством композиций каких-либо непрерывных функций двух переменных (следует отметить, что всякая функция конечного числа переменных является композицией разрывных функций двух переменных). Д. Гильбертом была показана невозможность получения всех аналитич. ций трех переменных в виде композиций аналитич. ций двух переменных. Он же для уравнения 9-й степени доказал [5], что решение уравнения 9-й степени можно представить в виде композиции алгебраич. функций четырех переменных (вместо пяти, как это сразу следует из применения преобразования Чирнгаузена). Эти исследования были продолжены многими математиками (см. [6] - [19]).
А. Г. Витушкин в 1954 доказал [10], что если натуральные числа m, п, m1 и n1 удовлетворяют неравенству  , то можно указать праз дифференцируемую функцию тпеременных, непредставимую в виде композиции n1 раз дифференцируемых функций от m1 переменных. В частности, при всяком пможно указать функцию ппеременных наперед заданной гладкости, непредставимую композицией функций меньшего числа переменных той же гладкости. В этом смысле среди гладких функций любого числа переменных существуют функции, существенно зависящие от всех своих аргументов.
, то можно указать праз дифференцируемую функцию тпеременных, непредставимую в виде композиции n1 раз дифференцируемых функций от m1 переменных. В частности, при всяком пможно указать функцию ппеременных наперед заданной гладкости, непредставимую композицией функций меньшего числа переменных той же гладкости. В этом смысле среди гладких функций любого числа переменных существуют функции, существенно зависящие от всех своих аргументов.
В 1956 А. Н. Колмогоров показал [11], что всякая определенная на n-мерном (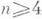 ) кубе непрерывная функция является композицией непрерывных функций трех переменных. Затем В. И. Арнольд уменьшил число переменных с трех до двух. Именно, он доказал [12], что любую непрерывную на кубе функцию трех переменных можно представить в виде композиции непрерывных функций двух переменных (и даже, более точно, в виде суммы 9 функций, каждая из к-рых является однократной композицией непрерывных функций двух переменных). Тем самым было показано, что каждая непрерывная на n-мерном (
) кубе непрерывная функция является композицией непрерывных функций трех переменных. Затем В. И. Арнольд уменьшил число переменных с трех до двух. Именно, он доказал [12], что любую непрерывную на кубе функцию трех переменных можно представить в виде композиции непрерывных функций двух переменных (и даже, более точно, в виде суммы 9 функций, каждая из к-рых является однократной композицией непрерывных функций двух переменных). Тем самым было показано, что каждая непрерывная на n-мерном ( ) кубе функция представит в виде композиции непрерывных функций двух переменных. Это явилось последним словом по опровержению гипотезы Гильберта о невозможности представления корней уравнения (*) в виде композиций непрерывных функций двух неременных. Работы А. Н. Колмогорова и В. И. Арнольда дали, в частности, положительный ответ на вопрос о представимости корней алгебраич. уравнений любой степени в виде композиции непрерывных функций не более чем двух переменных. Для композиций аналитич. и алгебраич. функций аналогичный вопрос не решен. До сих пор (1983) неизвестно, являются ли корни уравнения (*) композицией аналитич. ций или нет.
) кубе функция представит в виде композиции непрерывных функций двух переменных. Это явилось последним словом по опровержению гипотезы Гильберта о невозможности представления корней уравнения (*) в виде композиций непрерывных функций двух неременных. Работы А. Н. Колмогорова и В. И. Арнольда дали, в частности, положительный ответ на вопрос о представимости корней алгебраич. уравнений любой степени в виде композиции непрерывных функций не более чем двух переменных. Для композиций аналитич. и алгебраич. функций аналогичный вопрос не решен. До сих пор (1983) неизвестно, являются ли корни уравнения (*) композицией аналитич. ций или нет.
Этот цикл работ завершает следующая теорема Колмогорова [13]: любая непрерывная функция гс переменных может быть получена с помощью композиций непрерывных функций одного переменного и единственной функции двух неременных g(x, y) = x+y;именно, он доказал, что любая функция f, непрерывная на n-мерном кубе, может быть представлена в виде
 ,
,
где функции hi и j ij - непрерывны, а функции j ij, кроме того, стандартны, т. е. не зависят от выбора функции f.
А. Г. Витушкин показал [14], что для любых конечных наборов непрерывных функций pk и непрерывно дифференцируемых функций qk, зависящих от ппеременных, k=1, 2,..., т, n =1, 2,..., существуют даже аналитич. ции гс переменных, не представимые композицией вида
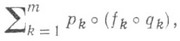
где fk - произвольные непрерывные функции одного переменного.
| |||
Свойство 1: (Первая теорема Вейерштрасса (Вейерштрасс Карл (1815-1897) - немецкий математик)). Функция, непрерывная на отрезке, ограничена на этом отрезке, т.е. на отрезке  выполняется условие - выполняется условие -  .
Доказательство этого свойства основано на том, что функция, непрерывная в точке .
Доказательство этого свойства основано на том, что функция, непрерывная в точке  , ограничена в некоторой ее окрестности, а если разбивать отрезок , ограничена в некоторой ее окрестности, а если разбивать отрезок  на бесконечное количество отрезков, которые “стягиваются” к точке на бесконечное количество отрезков, которые “стягиваются” к точке  , то образуется некоторая окрестность точки , то образуется некоторая окрестность точки  .
Свойство 2: Функция, непрерывная на отрезке .
Свойство 2: Функция, непрерывная на отрезке  , принимает на нем наибольшее и наименьшее значения.
Т.е. существуют такие значения , принимает на нем наибольшее и наименьшее значения.
Т.е. существуют такие значения  и и 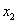 , что , что  , причем , причем  .
Отметим эти наибольшие и наименьшие значения функция может принимать на отрезке и несколько раз (например - .
Отметим эти наибольшие и наименьшие значения функция может принимать на отрезке и несколько раз (например -  ).
Разность между наибольшим и наименьшим значением функции на отрезке называется колебанием функции на отрезке.
Свойство 3: (Вторая теорема Больцано - Коши). Функция, непрерывная на отрезке ).
Разность между наибольшим и наименьшим значением функции на отрезке называется колебанием функции на отрезке.
Свойство 3: (Вторая теорема Больцано - Коши). Функция, непрерывная на отрезке  , принимает на этом отрезке все значения между двумя произвольными величинами.
Свойство 4: Если функция , принимает на этом отрезке все значения между двумя произвольными величинами.
Свойство 4: Если функция  непрерывна в точке непрерывна в точке  , то существует некоторая окрестность точки , то существует некоторая окрестность точки  , в которой функция сохраняет знак.
Свойство 5: (Первая теорема Больцано (1781-1848) - Коши). Если функция , в которой функция сохраняет знак.
Свойство 5: (Первая теорема Больцано (1781-1848) - Коши). Если функция  - непрерывная на отрезке - непрерывная на отрезке  и имеет на концах отрезка значения противоположных знаков, то существует такая точка внутри этого отрезка, где и имеет на концах отрезка значения противоположных знаков, то существует такая точка внутри этого отрезка, где  .
Т.е. если .
Т.е. если  , то , то  .
Определение. Функция .
Определение. Функция  называется равномерно непрерывной на отрезке называется равномерно непрерывной на отрезке  , если для любого , если для любого  существует существует  такое, что для любых точек такое, что для любых точек  и и  таких, что таких, что  верно неравенство верно неравенство  .
Отличие равномерной непрерывности от “обычной” в том, что для любого e существует свое .
Отличие равномерной непрерывности от “обычной” в том, что для любого e существует свое  , не зависящее от , не зависящее от  , а при “обычной” непрерывности , а при “обычной” непрерывности  зависит от зависит от 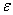 и и  .
Свойство 6: Теорема Кантора (Кантор Георг (1845-1918) - немецкий математик). Функция, непрерывная на отрезке, равномерно непрерывна на нем. (Это свойство справедливо только для отрезков, а не для интервалов и полуинтервалов.)
Свойство 7: Если функция .
Свойство 6: Теорема Кантора (Кантор Георг (1845-1918) - немецкий математик). Функция, непрерывная на отрезке, равномерно непрерывна на нем. (Это свойство справедливо только для отрезков, а не для интервалов и полуинтервалов.)
Свойство 7: Если функция  определена, монотонна и непрерывна на некотором промежутке, то и обратная ей функция определена, монотонна и непрерывна на некотором промежутке, то и обратная ей функция  тоже однозначна, монотонна и непрерывна.
Пример. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть. тоже однозначна, монотонна и непрерывна.
Пример. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.   в точке в точке  функция непрерывна в точке функция непрерывна в точке 
 точка разрыва 1 - го рода
точка разрыва 1 - го рода
|
| << Предыдушая | Следующая >> | |
| Р. Аллен. МАТЕМАТИЧЕСКАЯ ЭКОНОМИЯ, 1963 - перейти к содержанию учебника | ||
| 5.8. НЕПРЕРЫВНЫЕ РЕШЕНИЯ РАЗНОСТНЫХ УРАВНЕНИЙ | ||
| Разностное уравнение относительно Yx относится к любому ряду равноотстоящих (equally-spaced) значений независимой переменной х. Рассмотренные до сих пор дискретные решения применимы к одному частному ряду значений переменной х = 0, 1, 2, 3,... Однако разностное уравнение не ограничивается таким путем; отправной точкой для х может быть любое значение. Если отправной точкой является х = 0, то разностное уравнение порождает дискретное решение У0, Yx, У2, •••• Если в качестве начальной точки выбрать х =, то получится совершенно отличное дискретное решение Уі/2, Уз/2, Г5/2. Очевидно, что не существует ограничений для того, чтобы получить какое угодно число различных дискретных решений. Можно выбрать любое значение х между 0 и 1 в качестве начальной точки, и х можно заставить изменяться непрерывно. Спрашивается, можно ли все дискретные решения объединить в отдельное непрерывное решение, выражающее Yx в виде функции х, вообще для любого ряда равноотстоящих значений х. Например, предположим, что разностное уравнение характеризует уровень цен Yx в различные моменты времени х, а интервал значений х равен одному году. В этом случае х = 0, 1, 2,... может означать, например, конец года, и дискретное решение У будет тогда показывать изменение цен на 13 5 конец года от года к году. Но если положить х — y ' ~2 ' 2~' т0 П°ЛУЧИТСЯ другое дискретное решение Ух, которое будет показывать годовое изменение цен, но только на середину года. В обоих этих случаях, так же как и в других, подобных им, изменение цен в пределах года (например, сезонные колебания цен) в анализе не учитывается. Проблема сводится к тому, можно ли получить непрерывное решение для Yx, которое характеризовало бы полностью изменение цен во времени, то есть не только изменение цен год от года, но и изменение их в пределах каждого года. Уравнение первого порядка %(х, Yx, Ух-1) = 0 имеет дискретное решение Yx — Y(x\ Л), содержащее одну произвольную постоянную А. Какой бы частный ряд значений х мы ни рассматривали, А всегда можно выразить через начальное значение У. Если дано У0, решение относится к Yx при я = 0, 1, 2,...; если начальное значение задано Уі/2, то ре- V 13 5 шение относится к Ух при я = у, у,... и так далее для всех задаваемых Yx при х в "интервале 0<я<1. Теперь мы расширим понятие произвольного элемента; вместо одного заданного Ух, например У0 или Уі/2, мы будем рассматривать целую область задаваемых Yx при 0<я<1. Говоря более точно, вместо одной произвольной начальной величины, мы возьмем произвольную начальную функцию в области 0<я<1. Эта функция может начинаться с любого значения У0 и изменяться любым способом от х = 0 до х=\, возвращаясь при ж = 1 к начальному значению. Наша произвольная функция имеет период 1. Если продолжить наш пример с ценами, где Yx характеризует уровень цен, то произвольный элемент, который мы должны указать,— это вся область цен в пределах года, выраженных в форме сезонных изменений, начинающихся и кончающихся на одном и том же уровне. Если это сделано, разностное уравнение дает Yx для любых значений х, изменяющихся непрерывно. Обозначим через w(x) любую функцию с периодом 1, так что все значения w, разделенные единичным интервалом х, равны. Следовательно, для единичного интервала = Так же как и производная постоянной, разность функций периода 1 равна нулю. Постоянная исчезает при дифференцировании, функция периода 1 исчезает при исчислении дифференцирования по конечной разности. Таким образом, общее непрерывное решение уравнения % (х, Ух, Yx_t) = 0 имеет вид Yx = У (х{, w), где w — произвольная функция периода 1, которая может быть определена через начальные условия для Ух в интервале 0<ж< 1. Понятие непрерывного решения легко обобщить. Разностное уравнение второго порядка %(х, Yx, Yx_±, Yx_2) =0 имеет дискретное решение Yx = Y(x; Av А2) при ж = 0, 1, 2,..., где Аг и А2 — произвольные постоянные, которые можно отождествить с У0 и Уг Это же уравнение имеет непрерывное решение Yx = Y(x; ОУ2) для любого х, где и ^ — произвольные функции периода 1, которые можно выразить через начальные условия для Yx в двух интервалах 0<я<1 и 1<#<2. Очевидно, это можно обобщить для разностного уравнения любого порядка. Все, что раньше было сказано о произвольных постоянных или начальных значениях в дискретном решении, в равной степени относится и к произвольным функциям периода 1 в непрерывном решении. Решения разностных и дифференциальных уравнений имеют ряд отличающих их друг от друга черт. Например, область возможных решений линейных разностных уравнений (зависящих от показательной функции типа ах) вообще значительно шире или богаче, чем для линейных дифференциальных уравнений, решения которых зависят от показательной функции типа еах. Это ясно из нашего анализа в разделах 5.3 — 5.5. Однако сравнение, настоящей и предыдущей глав показывает, что методы решения линейных дифференциальных и разностных уравнений имеют очень много общего, хотя они в значительно большей степени освоены и разработаны для дифференциальных уравнений. Наконец, отметим, что разностные уравнения можно решать методами, аналогичными преобразованию Лапласа для дифференциальных уравнений (см. 4.7). Если положить YX = Y0 во всем интервале 0<#< 1, то частное дискретное решение Yx(x = 0, 1, 2,...) превращается в частное непрерывное решение. Это решение становится в таком случае ступенчатой функцией непрерывной переменной: Y(x) = Y0 (0<а<1); =УХ (1<я<2);..., и можно' применить метод преобразования Лапласа [4]. Альтернативно для дискретного ряда Yx преобразование можно определить через суммы — аналогично интегралу преобразования Лапласа для функции непрерывной переменной. Простым преобразованием такого типа является функция женератриса (generating function)32: со х=0 в которой коэффициенты при возрастающих степенях s образуют последовательность значений Yx. Решение разностных уравнений преобразованием Yx в У (я) очень похоже на преобразование Лапласа в случае дифференциальных уравнений (см. [5], особенно пример там на стр. 194). |
Дата добавления: 2015-09-10; просмотров: 106 | Поможем написать вашу работу | Нарушение авторских прав |